Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tra gu gồ được mà,hỏi làm gì cho mệt chớ,tìm được cách làm trên gu gồ là áp dụng vào bài thôi
noi A vs C ,BvsC
ap dung tinh chat duong trug binh cua tam giac
AM=EN
MN=FE
MNEF la hinh thoi

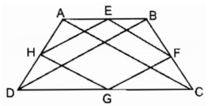
Trong ∆ ABD ta có:
E là trung điểm của AB (gt)
H là trung điểm của AD (gt)
nên EH là đường trung bình của ∆ ABD
⇒ EH // BD và EH = 1/2 BD (tính chất đường trung bình của tam giác) (1)
- Trong ∆ CBD ta có:
F là trung điểm của BC (gt)
G là trung điểm của CD (gt)
nên FG là đường trung bình của ∆ CBD
⇒ FG // BD và FG = 1/2 BD (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: EH // FG và EH = FG
Suy ra: Tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Trong ∆ ABC ta có:
EF là đường trung bình
⇒ EF = 1/2 AC (tính chất đường trung bình của tam giác) (3)
AC = BD (tính chất hình thang cân) (4)
Từ (1), (3) và (4) suy ra: EH = EF
Vậy : Tứ giác EFGH là hình thoi.

Xét tam giác ABC có:
M là trung điểm AB
N là trung điểm BC
=> MN là đường trung bình
=> MN//AC và \(MN=\dfrac{1}{2}AC\)(1)
Xét tam giác ADC có:
F là trung điểm AD
E là trung điểm DC
=> EF là đường trung bình
=> EF//AC và \(EF=\dfrac{1}{2}AC\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrowđpcm\)

Bài 1:
a: Xét tứ giác ABEF có
BE//AF
BE=AF
BE=BA
Do đó: ABEF là hình thoi
b: Xét ΔBIE có BI=BE
nên ΔBIE cân tại B
mà góc IBE=60 độ
nên ΔBIE đều
=>góc I=60 độ
Xét tứ giác AFEI có
EF//AI
góc I=góc A
Do đó AFEI là hình thang cân
c: Xét ΔBAD có
BF là đường trung tuyến
BF=AD/2
Do đó: ΔBAD vuông tại B
=>DB vuông góc với BI
Xét tứ giác BICD có
BI//CD
BI=CD
Do đó: BICD là hình bình hành
mà DB vuông góc với BI
nên BICD là hình chữ nhật
d: Xét ΔAED có
EF la trung tuyến
FE=DA/2
Do đó: ΔAED vuông tại E
=>góc AED=90 độ

a, Vì O là trung điểm EF
MN qua O //AB//CD
=>M là trung điểm AD, N là TD BC

a) Ta có: AB//CD(gt)
mà E∈AB và F∈CD
nên AE//DF và EB//FC
Xét tứ giác AEFD có AE//DF(cmt)
nên AEFD là hình thang có hai đáy là AE và DF(Định nghĩa hình thang)
Hình thang AEFD(AE//DF) có
O là trung điểm của EF(gt)
OM//AE//DF(MN//AB//DC, E∈AB, O∈MN, F∈DC)
Do đó: M là trung điểm của AD(Định lí 3 về đường trung bình của hình thang)
Xét tứ giác BEFC có BE//FC(cmt)
nên BEFC là hình thang có hai đáy là BE và FC(Định nghĩa hình thang)
Hình thang BEFC(BE//FC) có
O là trung điểm của EF(gt)
ON//EB//FC(MN//AB//DC, E∈AB, O∈MN, F∈CD)
Do đó: N là trung điểm của BC(Định lí 3 về đường trung bình của hình thang)
Xét ΔABD có
M là trung điểm của AD(cmt)
E là trung điểm của AB(gt)
Do đó: ME là đường trung bình của ΔABD(Định nghĩa đường trung bình của tam giác)
⇒ME//BD và ME=BD2ME=BD2(Định lí 2 về đường trung bình của tam giác)(1)
Xét ΔBDC có
N là trung điểm của BC(cmt)
F là trung điểm của CD(gt)
Do đó: NF là đường trung bình của ΔBDC(Định nghĩa đường trung bình của tam giác)
⇒NF//BD và NF=BD2NF=BD2(Định lí 2 về đường trung bình của tam giác)(2)
Từ (1) và (2) suy ra ME//NF và ME=NF
Xét tứ giác EMFN có ME//NF(cmt) và ME=NF(cmt)
nên EMFN là hình bình hành(Dấu hiệu nhận biết hình bình hành)
b) Xét ΔBAC có
E là trung điểm của AB(gt)
N là trung điểm của BC(cmt)
Do đó: EN là đường trung bình của ΔBAC(Định nghĩa đường trung bình của tam giác)
⇒EN//AC và EN=AC2EN=AC2(Định lí 2 về đường trung bình của tam giác)
Hình bình hành EMFN trở thành hình thoi khi EM=EN
mà EM=BD2EM=BD2(cmt) và EN=AC2EN=AC2(cmt)
nên BD=AC
Vậy: Khi hình thang ABCD có thêm điều kiện BD=AC thì EMFN là hình thoi

D C B A N M E F
\(\Delta BCD\)có :
\(BE=EC\)( gt )
\(DF=FC\)( gt )
\(\Rightarrow\)EF - đtb t/g BCD
\(\Delta ADB\)có :
\(AM=MD\)( gt )
\(AN=NB\)( gt )
\(\Rightarrow\)MN - đtb t/g ADB ( 2 )
Từ ( 1 ) ; ( 2 ) suy ra EF = Mn ; EF // MN
\(\Rightarrow\)MNEF - hbh
đến đây tự chứng minh tiếp hình thoi nha