Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kéo dài AD và BC, chúng cắt nhau tại M, dựng đường cao DH.
⇒ tam giác ABM đều.⇒AB=AM=4,5⇒DC=AM-AD=4,5-2=2,5Xét tam giác ADH vuông tại D có ADH=30AH=1/2AD=1/2.2=1Mặt khác ta có:DH²=AD²-AH²(theo định lý PITAGO)⇒DH²=4-1=3⇒DH=√3⇒Sabcd=(DC+AB).DH/2=(2,5+4,5).√3/2=7√3/2
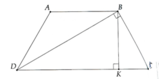
Hạ \(DH\perp AB,CK\perp AB\).
Tam giác \(AHD\)vuông tại \(H\)có\(\widehat{ADH}=30^o\)nên \(AH=\frac{1}{2}AD=1\left(cm\right)\)
\(HD=\sqrt{AD^2-AH^2}=\sqrt{2^2-1^2}=\sqrt{3}\left(cm\right)\)
Tương tự \(BK=1\left(cm\right)\).
\(DC=HK=AB-AH-BK=2,5\left(cm\right)\)
\(S_{ABCD}=\frac{AB+CD}{2}.DH=\frac{4,5+2,5}{2}.\sqrt{3}=\frac{7\sqrt{3}}{2}\left(cm^2\right)\)

. a) HS tự chứng minh
b) Kẻ đường cao AH, BK,chứng minh được DH = CK
Ta được H D = C D − A B 2 = 3 c m
Þ AH = 4cm Þ SABCD = 20cm2

Hạ CH và DK vuông góc với AB
Ta có:
A K = B H = 1 2 A D = 1 c m
Từ đó: CD = 2,5cm
C H = 3 c m
S A B C D = A B + C D . C D 2 = 7 3 2 c m 2


A B C D E F
Bài làm:
Từ D,E kẻ DE,CF vuông góc với AB \(\left(E,F\in AB\right)\)
Xét trong Δ vuông ADE tại D có góc A bằng 60 độ
=> \(\widehat{ADE}=30^0\)
Vì tam giác ADE có: \(\hept{\begin{cases}\widehat{A}=60^0\\\widehat{ADE}=30^0\\\widehat{AED}=90^0\end{cases}}\) => \(AE=\frac{AD}{2}=\frac{2}{2}=1\left(cm\right)\)
Tương tự tính được: \(BF=1\left(cm\right)\)
=> \(FE=AB-AE-BF=4,5-2=2,5\left(cm\right)\)
Vì DC // FE và DE // FC nên theo t/c đoạn chắn
=> DC = FE = 2,5 (cm)
Áp dụng định lý Pytago ta được: \(DE^2=AD^2-AE^2=2^2-1^2=3\left(cm\right)\)
=> \(DE=\sqrt{3}\left(cm\right)\)
Diện tích hình thang cân ABCD là: \(\frac{\left(AB+CD\right).DE}{2}=\frac{7\sqrt{3}}{2}\left(cm^2\right)\)
Giải
Kẻ DH vuông góc với AB
\(\sin\widehat{A}=\frac{DH}{AD}\)
\(\Leftrightarrow\sin60^o=\frac{DH}{2}\Rightarrow DH=\sqrt{3}\)
\(\cos A=\frac{AH}{AD}\)
\(AH=\cos60^o.2\)
\(\Rightarrow DC=AB-1-1=4,5-2=2,5\)
\(S\)ABCD=\(\frac{1}{2}.\sqrt{3}.\left(4,5+2,5\right)\)
\(=\frac{7\sqrt{3}}{2}\)

a) DDBC vuông có B C D ^ = 2 B D C ^ nên A D C ^ = B C D ^ = 60 0 và D A B ^ = C B A ^ = 120 0
b) Tính được DC = 2.BC = 12cm, suy ra PABCD = 30cm.
Hạ đường cao BK, ta có BK = 3 3 c m .
Vậy SABCD = 27 3 c m 2