Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Hung nguyenPhạm Hoàng GiangDƯƠNG PHAN KHÁNH DƯƠNGMysterious PersonPhùng Khánh LinhTRẦN MINH HOÀNGAkai Haruma
a: Xét ΔCBD có CN/CD=CM/CB
nên NM//BD và NM=BD/2
=>BD=15cm
b: NM=BD/2
mà NM=NK/2
nên BD=NK
c: Xét ΔEDC có
B là trung điểm của ED
BK//DC
DO đó: K là trung điểm của CE
Hình bạn tự vẽ nha.
a)Xét \(\Delta BCD\), có:
M,N lần lượt là trung điểm của BC,CD.
\(\Rightarrow MN\) là đường trung bình của \(\Delta BCD\)
\(\Rightarrow MN=\dfrac{1}{2}BD\Rightarrow BD=2MN=2.7,5=15\left(cm\right)\)
b)Xét \(\Delta BKM\) và \(\Delta CNM\), có:
\(\widehat{BMK}=\widehat{CMN}\)(đối đỉnh)
\(MB=MC\)(M là trung điểm của BC)
\(\widehat{KBM}=\widehat{NCM}\)(so le trong và AK//DC vì K nằm trên AB mà AB//CD)
Do đó:\(\Delta BKM=\Delta CNM\left(g.c.g\right)\)
\(\Rightarrow KB=NC\)(hai cạnh tương ứng)
Mà \(ND=NC\)(N là trung điểm của DC)
\(\Rightarrow KB=ND_{\left(1\right)}\)
Lại có:BK//DN(vì K nằm trên AB, N nằm tên CD mà AB//CD)
\(\Rightarrow BKND\) là hình thang\(_{\left(2\right)}\)
Từ (1) và (2) \(\Rightarrow NK=BD\)(theo nhận xét)
c)Xét \(\Delta CDE\), có:
B là trung điểm của DE (do D đx với E qua B)
BK//CD(do K nằm trên AB mà AB//CD)
\(\Rightarrow BK\) là đường trung bình của \(\Delta CDE\)
\(\Rightarrow K\) là trung điểm của CE(đpcm)
Vì ABCD là hình thang cân có AB // CD nên:
AC = BD (1)
Xét ΔADC và ΔBCD, ta có:
AC = BD (chứng minh trên)
AD = BC (ABCD cân)
CD cạnh chung
Suy ra: △ ADC = △ BCD (c.c.c)
Suy ra : ∠ (ACD) = ∠ ( BDC)
Hay ∠ (OCD) = ∠ ( ODC)
Suy ra tam giác OCD cân tại O
Suy ra: OD = OC (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: OA = OB
Ta có: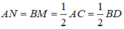 
Mà OA = OB ⇒ OM = ON
Lại có: MD = 3MO (gt) ⇒ NC = 3NO
Trong ΔOCD, ta có: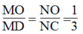 
Suy ra: MN // CD (Định lí đảo của định lí Ta-lét)
Ta có: OD = OM + MD = OM + 3OM = 4OM
Trong ΔOCD, ta có: MN // CD
Suy ra: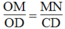 
Hệ quả định lí Ta-lét)
Suy ra: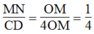 
Suy ra: MN = 1/4 CD = 1/4 .5,6 = 1,4 (cm)
Ta có: MB = MD (gt)
Suy ra: MB = 3OM hay OB = 2OM
Lại có: AB // CD (gt) suy ra: MN // AB
Ta có: MN // AB, áp dụng hệ quả định lý Ta – let ta được:
(Hệ quả định lí Ta-lét)
Suy ra: 
Vậy: AB = 2MN = 2.1,4 = 2,8(cm)
Trung điểm cạnh BCH là j dẹ bạn.
BC thôi ạ. Do bàn phím của mình nó chỉnh