Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Gọi M' và N' là giao điểm của tia AM và BN với CD.
Ta có: ∠(M') = ∠A2(sole trong)
∠A1= ∠A2(gt)
⇒ ∠(M') = ∠A1nên ΔADM' cân tại D
* DM là phân giác của ∠(ADM' )
Suy ra: DM là đường trung tuyến (tính chất tam giác cân)
⇒ AM = MM'
∠(N') = ∠B1nên ΔBCN' cân tại C.
* CN là phân giác của ∠(BCN')
Suy ra: CN là đường trung tuyến (tính chất tam giác cân)
⇒ PN = NN'
Suy ra: MN là đường trung bình của hình thang ABN'M'
⇒ MN = M'N' (tính chất đường trung hình hình thang)
Hay MN//CD
b)MN=AB+M′N′/2 (tính chất đường trung bình của hình thang)
⇒MN=AB+M′D+CD+CN′/2(1)
Mà M′D=AD,CN′=BC. Thay vào (1)
MN=AB+AD+CD+BC/2=a+d+c+b/2

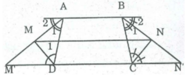
Gọi M' và N' là giao điểm của tia AM và BN với CD.
Ta có: ∠ (M') = ∠ A 2 (sole trong)
∠ A 1 = ∠ A 2 (gt)
⇒ ∠ (M') = ∠ A 1 nên ∆ ADM' cân tại D
* DM là phân giác của ∠ (ADM' )
Suy ra: DM là đường trung tuyến (tính chất tam giác cân)
⇒ AM = MM'
∠ (N') = ∠ B 1 nên ∆ BCN' cân tại C.
* CN là phân giác của ∠ (BCN')
Suy ra: CN là đường trung tuyến (tính chất tam giác cân)
⇒ BN = NN'
Suy ra: MN là đường trung bình của hình thang ABN'M'
⇒ MN // M'N' (tính chất đường trung hình hình thang)
Hay MN//CD

a) Gọi E, F lần lượt là giao điểm của AM và CD, BN và CD
Ta có : AB//CD (gt) => E = A1 (so le trong)
Mà A1 =A2 (gt)
Nên A2 = E
Xét ΔADE cân tại D, có DM là p/giác nên DM đồng thời là trung tuyến
=>AM= EM
Chứng minh tương tự, ta được :
BN = FN
Xét hình thang ABEF có : AM=BN(cm trên)
BN=FN(cm trên)
Do đó MN là đường TB của HÌNH thang ABEF
=> MN= \(\frac{EF+AB}{2}\)
MN//AB//EF Vậy MN// CD(đpcm)
b)Do ED= AD; BC=FC
Mà ED + DC + CF = EF
Nên AD + DC + BC = EF
Lại có MN \(\frac{EF+AB}{2}\)(CM trên)
Suy ra MN= \(\frac{AD+DC+BC+AB}{2}\)\(=\frac{a+b+c+d}{2}\)