Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a) Gọi phương trình đường thẳng có dạng $y=ax+b$ $(d)$
Vì \(B,C\in (d)\Rightarrow \left\{\begin{matrix} 3=2a+b\\ -3=-4a+b\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=1\\ b=1\end{matrix}\right.\Rightarrow y=x+1\)
Vậy PT đường thẳng chứa cạnh $BC$ có dạng $y=x+1$
b) Tương tự, ta lập được phương trình đường thẳng chứa cạnh $AC$ là \((d_1):y=\frac{2x}{5}-\frac{7}{5}\).
Gọi PT đường cao đi qua $B$ của tam giác $ABC$ là \((d'):y=ax+b\)
Vì \((d')\perp (d_1)\Rightarrow \frac{2}{5}a=-1\Rightarrow a=\frac{-5}{2}\).
Mặt khác \(B\in (d')\Rightarrow 3=\frac{-5}{2}.2+b\Rightarrow b=8\)
\(\Rightarrow (d'):y=\frac{-5x}{2}+8\)
c) Gọi điểm thỏa mãn ĐKĐB là $M(a,b)$
Ta có: \(M\in (\Delta)\Rightarrow 2a+b-3=0\) $(1)$
$M$ cách đều $A,B$ \(\Rightarrow MA^2=MB^2\Rightarrow (a-1)^2+(b+1)^2=(a-2)^2+(b-3)^2\)
\(\Leftrightarrow 2-2a+2b=13-4a-6b\)
\(\Leftrightarrow 11-2a-8b=0(2)\)
Từ \((1);(2)\Rightarrow \left\{\begin{matrix} a=\frac{13}{14}\\ b=\frac{8}{7}\end{matrix}\right.\Rightarrow M\left ( \frac{13}{14};\frac{8}{7} \right )\)
con nếu đề bài cho 1 điểm và phương trình đường thẳng của tam giác muốn tìm phương trình đường cao còn lại vầ các cạnh thj làm thế nào

làm đc chưa bạn...
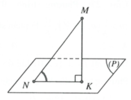
gọiE là tđ AD
suy ra NA = NH = NMNM
gọi F là tđ AM thì c/m đc KN KM KA KD bằng nhau
vậy AMN cân vuông tại N

4a.
Số tự nhiên là A, ta có:
A = 7m + 5
A = 13n + 4
=>
A + 9 = 7m + 14 = 7(m + 2)
A + 9 = 13n + 13 = 13(n+1)
vậy A + 9 là bội số chung của 7 và 13
=> A + 9 = k.7.13 = 91k
<=> A = 91k - 9 = 91(k-1) + 82
vậy A chia cho 91 dư 82
4b.
Giả sử p là 1 số nguyên tố >3, do p không chia hết cho 3 nên p có dạng 3k + 1 hoặc 3k + 2
Vì p +4 là số nguyên tố nên p không thể có dạng 3k + 2
Vậy p có dạng 3k +1.
=> p + 8 = 3k + 9 chia hết cho 3 nên nó là hợp số.






Đáp án D
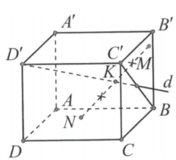
Ý tưởng: 1 - MN phải chăng sẽ là hai điểm đặc biệt nào đó
2 – Khi nhận ra M là trung điểm của BA’ thì ta tiến hành tính toán MN qua điểm A’ bằng cách lấy P thuộc BC’!
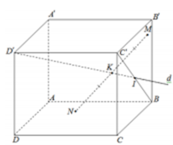
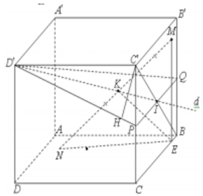
Dễ có mặt phẳng (BA’C’) vuông góc với AB’. Do đó để MN là nhỏ nhất thì M là giao của AB’ và BA’, N là điểm thuộc BC’ sao cho góc giữa MN và (A’B’C’D’) là 30 ° . Gọi P là điểm thuộc BC’sao cho A’P cũng hợp với mặt phẳng đáy một góc 30 ° , khi đó MN là đường trung bình của tam giác BA’P nên M N = 1 2 A ' P .
Giả sử độ dài đoạn B’H = x, khi đó PH = HC’ = a – x (tam giác PC’H vuông cân tại C’), và A ' H = A ' B ' 2 + B ' H 2 = a 2 + x 2 . Theo điều ta đã giả sử ở trên thì góc giữa A’P và (A’B’C’D’) = 30 ° , do đó
tan P A ' H ^ = P H A ' H = a − x a 2 + x 2 = 3 3 hay a 2 + x 2 = 3 a − x (1)
Mặt khác ta lại có
A ' P = A ' H 2 + H P 2 = a 2 + x 2 + ( a − x ) 2 = 4 a − x 2 = 2 a − x (2)
Từ (1) và (2) ta tính được A ' P = 4 a 5 + 1 . Từ đây ta rút ra được M N = 2 a 5 + 1 .
Chọn phương án D.