Cho hình lập phương ABCD.A'B'C'D'. Chứng minh rằng:a) Mặt phẳng (AB'C'D) vuông góc với (BCD...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

PT

Pham Trong Bach

10 tháng 2 2018

Cho hình lập phương ABCD.A'B'C'D'. Chứng minh rằng:

a) Mặt phẳng (AB'C'D) vuông góc với (BCD'A')

b) Đường thẳng AC' vuông góc với mặt phẳng (A'BD)

#Hỏi cộng đồng OLM #Toán lớp 11

1

CM

Cao Minh Tâm

10 tháng 2 2018

Giải bài 5 trang 114 sgk Hình học 11 | Để học tốt Toán 11

Giải bài 5 trang 114 sgk Hình học 11 | Để học tốt Toán 11

Giải bài 5 trang 114 sgk Hình học 11 | Để học tốt Toán 11

Các câu hỏi dưới đây có thể giống với câu hỏi trên

SG

Sách Giáo Khoa

31 tháng 3 2017

Cho lập phương ABCD.A'B'C'D'. Chứng minh rằng :

a) Mặt phẳng (AB'C'D) vuông góc với mặt phẳng (BCD'A')

b) Đường thẳng AC' vuông góc với mặt phẳng (A'BD)

#Hỏi cộng đồng OLM #Toán lớp 11

1

QD

Quang Duy

31 tháng 3 2017

Giải bài 5 trang 114 sgk Hình học 11 | Để học tốt Toán 11

Giải bài 5 trang 114 sgk Hình học 11 | Để học tốt Toán 11

SG

Sách Giáo Khoa

22 tháng 5 2017

a) Cho hình lập phương ABCD. A'B'C'D' cạnh a. Chứng minh rằng đường thẳng AC' vuông góc với mặt phẳng (A'BD) và mặt phẳng (ACC'A') vuông góc với mặt phẳng (A'BD)

b) Tính đường chéo AC' của hình lập phương đã cho

#Hỏi cộng đồng OLM #Toán lớp 11

1

NT

Nguyen Thuy Hoa

26 tháng 5 2017

Vectơ trong không gian, Quan hệ vuông góc

b) Ta có ACC' là tam giác vuông có cạnh \(AC=a\sqrt{2},CC'=a\)

Vậy \(AC'^2=AC^2+CC^2\Rightarrow AC'^2=2a^2+a^2=3a^2\)

Vậy \(AC'=a\sqrt{3}\)

SG

Sách Giáo Khoa

22 tháng 5 2017

Cho tam giác ABC. Gọi \(\left(\alpha\right)\) là mặt phẳng vuông góc với đường thẳng CA tại A và \(\left(\beta\right)\) là mặt phẳng vuông góc với đường thẳng CB tại B. Chứng minh rằng hai mặt phẳng \(\left(\alpha\right)\) và \(\left(\beta\right)\) cắt nhau và giao tuyến d của chúng vuông góc với mặt phẳng (ABC)...

#Hỏi cộng đồng OLM #Toán lớp 11

1

NT

Nguyen Thuy Hoa

26 tháng 5 2017

Hỏi đáp Toán

PT

Pham Trong Bach

25 tháng 1 2017

Cho hình lập phương ABCD.A’B’C’D’ cạnh a.

a) Chứng minh rằng đường thẳng AC’ vuông góc với mặt phẳng (A’BD) và mặt phẳng (ACC’A’) vuông góc với mặt phẳng (A’BD).

b) Tính đường chéo AC’ của hình lập phương đã cho.

#Hỏi cộng đồng OLM #Toán lớp 11

1

CM

Cao Minh Tâm

25 tháng 1 2017

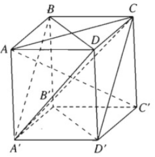
Giải sách bài tập Toán 11 | Giải sbt Toán 11

a) Ta có AB = AD = AA′ = a

và C ′ B = C ′ D = C ′ A ′ = a 2

Vì hai điểm A và C’ cách đều ba đỉnh của tam giác A’BD nên A và C’ thuộc trục đường tròn ngoại tiếp tam giác BDA’ . Vậy AC′ ⊥ (BDA′). Mặt khác vì mặt phẳng (ACC’A’) chứa đường thẳng AC’ mà AC′ ⊥ (BDA′) nên ta suy ra mặt phẳng (ACC’A’) vuông góc với mặt phẳng (BDA’)

b) Ta có ACC’ là tam giác vuông có cạnh A C = a 2 và CC’ = a

Vậy A C ′ 2 = A C 2 + C C ′ 2

⇒ A C ′ 2 = 2 a 2 + a 2 = 3 a 2 . V ậ y A C ′ = a 3 .

NM

Nguyễn Minh Huy

12 tháng 3 2021 - olm

cho hình chóp S.ABCD với đáy là hình chữ nhật,AD=2a,AB=a; O là giao điểm của AC và BD, SO vuông góc với mặt phẳng (ABCD) và SO=a/2. Gọi M là trung điểm của BC.

a)Chứng minh SM vuông góc mặt phẳng (SAD)

b) Gọi \(\phi\) là góc giữa đường thẳng SC và mặt phẳng (SAD), tính sin\(\phi\)

#Hỏi cộng đồng OLM #Toán lớp 11

0

SG

Sách Giáo Khoa

22 tháng 5 2017

Hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng nhau. Chứng minh rằng \(AC\perp B'D',AB'\perp CD',AD'\perp CB'\). Khi nào mặt phẳng (AA'C'C) vuông góc với mặt phẳng (BB'D'D) ?

#Hỏi cộng đồng OLM #Toán lớp 11

1

NT

Nguyen Thuy Hoa

26 tháng 5 2017

Vectơ trong không gian, Quan hệ vuông góc

SG

Sách Giáo Khoa

31 tháng 3 2017

Trong mặt phẳng \(\left(\alpha\right)\) cho tam giác ABC vuông ở B. Một đoạn thẳng AD vuông góc với \(\left(\alpha\right)\) tại A. Chứng minh rằng : a) \(\widehat{ABD}\) là góc giữa hai mặt phẳng (ABC) và (DBC) b) Mặt phẳng (ABD) vuông góc với mặt phẳng (BDC) c) HK// BC với H và K lần lượt là giao điểm của DB và DC với mặt phẳng (P) đi qua A và vuông gcs với...

#Hỏi cộng đồng OLM #Toán lớp 11

1

QD

Quang Duy

31 tháng 3 2017

Giải bài 3 trang 113 sgk Hình học 11 | Để học tốt Toán 11

Giải bài 3 trang 113 sgk Hình học 11 | Để học tốt Toán 11

SG

Sách Giáo Khoa

31 tháng 3 2017

Hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a và có góc \(\widehat{BAD}=60^0\). Gọi O là giao điểm của AC và BD. Đường thẳng SO vuông góc với mặt phẳng (ABCD) và \(SO=\dfrac{3a}{4}\). Gọi E là trung điểm của đoạn BC, F là trung điểm của BE a) Chứng minh mặt phẳng (SOF) vuông góc với mặt phẳng (SBC) b) Tính các khoảng cách từ O và A đến mặt phẳng...

#Hỏi cộng đồng OLM #Toán lớp 11

1

QD

Quang Duy

31 tháng 3 2017

Giải bài 4 trang 121 sgk Hình học 11 | Để học tốt Toán 11

Giải bài 4 trang 121 sgk Hình học 11 | Để học tốt Toán 11

SG

Sách Giáo Khoa

31 tháng 3 2017

Cho hình chóp S.ABCD có đáy ABCD là một hình thoi tâm I cạnh a và có góc A bằng \(60^0\), cạnh \(SC=\dfrac{a\sqrt{6}}{2}\) và SC vuông góc với mặt phẳng (ABCD) a) Chứng minh mặt phẳng (SBD) vuông góc với mặt phẳng (SAC) b) Trong tam giác SCA kẻ IK vuông góc với SA tại K. Hãy tính độ dài IK c) Chứng minh \(\widehat{BKD}=90^0\) và từ đó suy ra mặt phẳng (SAB) vuông góc với mặt phẳng...

#Hỏi cộng đồng OLM #Toán lớp 11

1

QD

Quang Duy

31 tháng 3 2017

Giải bài 11 trang 114 sgk Hình học 11 | Để học tốt Toán 11

Giải bài 11 trang 114 sgk Hình học 11 | Để học tốt Toán 11

Giải bài 11 trang 114 sgk Hình học 11 | Để học tốt Toán 11

Giải bài 11 trang 114 sgk Hình học 11 | Để học tốt Toán 11