Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kiến thức mình còn kém nên không biết làm, nhờ các cậu giúp cho !
Đề của mình được trích từ Đề thi thử vào lớp 6, năm 2014 !
A B C D M N P Q
Nối B với D; B với P
Ta có SBPC = \(\frac{2}{3}\)SBDC (chung chiều cao hạ từ đỉnh B xuống CD; đáy CP = \(\frac{2}{3}\) CD )
SNPC = \(\frac{2}{3}\)SBPC (chung chiều cao hạ từ đỉnh P xuống BC; đáy NC = \(\frac{2}{3}\) CB)
=> SNPC = \(\frac{2}{3}\) x \(\frac{2}{3}\)SBDC = \(\frac{4}{9}\)SBDC = \(\frac{4}{9}\)x \(\frac{1}{2}\) SABCD = \(\frac{2}{9}\)SABCD
Tương tự; SBMN = \(\frac{1}{24}\)SABCD; SAMQ = \(\frac{9}{32}\)SABCD; SDPQ = \(\frac{1}{24}\) SABCD
vậy SNPC + SBMN + SAMQ + SDPQ = \(\left(\frac{2}{9}+\frac{1}{24}+\frac{9}{32}+\frac{1}{24}\right)\)SABCD = \(\frac{169}{288}\)SABCD = \(\frac{169}{288}\). 1152 = 676
=> S MNPQ = 1152 - 676 = 476 cm vuông

\(S_{AQM}=\frac{1}{2}\times AQ\times AM=\frac{1}{2}\times\frac{3}{4}\times AB\times\frac{1}{2}\times AD=\frac{3}{16}\times AB\times AD=\frac{3}{16}\times S_{ABCD}\)
\(S_{BMN}=\frac{1}{2}\times BM\times BN=\frac{1}{2}\times\frac{1}{4}\times BA\times\frac{1}{4}\times BC=\frac{1}{16}\times BA\times BC=\frac{1}{16}\times S_{ABCD}\)
\(S_{CPN}=\frac{1}{2}\times CP\times CN=\frac{1}{2}\times\frac{1}{3}\times CD\times\frac{3}{4}\times CB=\frac{1}{8}\times CD\times CB=\frac{1}{8}\times S_{ABCD}\)
\(S_{DPQ}=\frac{1}{2}\times DP\times DQ=\frac{1}{2}\times\frac{2}{3}\times DC\times\frac{1}{2}\times DA=\frac{1}{6}\times DA\times DC=\frac{1}{6}\times S_{ABCD}\)
\(S_{AMQ}+S_{BNM}+S_{CPN}+S_{DPQ}+S_{MNPQ}=S_{ABCD}\)
\(\Leftrightarrow S_{MNPQ}=S_{ABCD}-S_{AMQ}-S_{BNM}-S_{CPN}-S_{DPQ}\)
\(=\left(1-\frac{3}{16}-\frac{1}{16}-\frac{1}{8}-\frac{1}{6}\right)\times S_{ABCD}\)
\(=\frac{11}{24}\times S_{ABCD}\)
\(=440\left(cm^2\right)\)

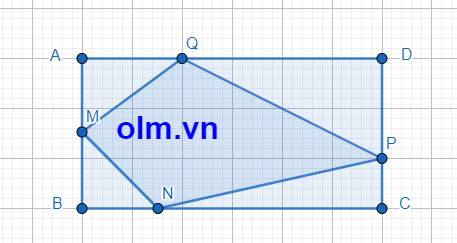
Cho hình chữ nhật ABCD có diện tích 216 cm2. Trên các cạnh AB, BC, CD và DA lần lượt lấy các điểm M, N, P, Q sao cho AM = MB, BN = 2/3 BC, CP = 2/3 CD và DQ = QA. Tính diện tích hình MNPQ?

A B C D M N P Q
Hình tớ vẽ hơi xấu, bạn thông cảm nhé.
Ta có \(S\Delta AMQ=\dfrac{1}{2}.AM.AQ=\dfrac{1}{2}.\dfrac{1}{2}AB.\dfrac{1}{3}AD\)
\(=\dfrac{1}{12}.288=24\left(cm^2\right)\)
\(S\Delta MBN=\dfrac{1}{2}MB.BN=\dfrac{1}{2}.\dfrac{1}{2}AB.\dfrac{1}{4}BC\)
\(=\dfrac{1}{16}.288=18\left(cm^2\right)\)
\(S\Delta QDP=\dfrac{1}{2}QD.DP=\dfrac{1}{2}.\dfrac{2}{3}AD.\dfrac{2}{3}DC\)
\(=\dfrac{2}{9}.288=64\left(cm^2\right)\)
\(S\Delta NPC=\dfrac{1}{2}.NC.CP=\dfrac{1}{2}.\dfrac{3}{4}BC.\dfrac{1}{3}.DC\)
\(=\dfrac{1}{8}.288=36\left(cm^2\right)\)
\(S_{MNPQ}=288-36-64-18-24=146\left(cm^2\right)\)
DQ + QA = DA ⇒ QA = DA - DQ = DA - \(\dfrac{2}{3}\)DA = \(\dfrac{1}{3}\)DA
SAMQ = \(\dfrac{1}{3}\)SADM( Vì hai tam giác có chung chiều cao hạ từ đỉnh M xuống đáy AD và AQ = \(\dfrac{1}{3}\)AD)
SADM = \(\dfrac{1}{2}\)SABD(vì hai tam giác có chung chiều cao hạ từ đỉnh D xuống đáy AB và AM = \(\dfrac{1}{2}\)AB)
SABD = \(\dfrac{1}{2}\)SABCD(vì ABCD là hình chữ nhật)
⇒SAMQ = \(\dfrac{1}{3}\times\dfrac{1}{2}\times\dfrac{1}{2}\)\(\times\)SABCD = 288 \(\times\) \(\dfrac{1}{12}\)= 24 (cm2)
SDPQ = \(\dfrac{2}{3}\)SADP(vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy AD và DQ = \(\dfrac{2}{3}\)DA)
DP = DC - CP = DC - \(\dfrac{1}{3}\)DC = \(\dfrac{2}{3}\)DC
SADP = \(\dfrac{2}{3}\)SACD(Vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy DC và DP = \(\dfrac{2}{3}\) DC)
SACD = \(\dfrac{1}{2}\)SABCD
⇒SDPQ = \(\dfrac{2}{3}\times\dfrac{2}{3}\times\)\(\dfrac{1}{2}\)\(\times\)SABCD = 288 \(\times\) \(\dfrac{2}{9}\)= 64 (cm2)
CN = BC - BN = BC - \(\dfrac{1}{4}\)BC = \(\dfrac{3}{4}\)BC
SCNP = \(\dfrac{3}{4}\)SCBP(vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy BC và CN = \(\dfrac{3}{4}\)BC)
SCBP = \(\dfrac{1}{3}\)SBCD(vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đấy CD và CP = \(\dfrac{1}{3}\) CD)
SBCD = \(\dfrac{1}{2}\)SABCD (vì ABCD là hình chữ nhật)
⇒SCNP = \(\dfrac{3}{4}\times\dfrac{1}{3}\times\dfrac{1}{2}\) SABCD = 288 \(\times\) \(\dfrac{1}{8}\) = 36 (cm2)
SBMN = \(\dfrac{1}{4}\)SBCM (Vì hai tam giác có chung đường cao hạ từ đỉnh M xuống đáy BC và BN = \(\dfrac{1}{4}\)BC)
SBCM = \(\dfrac{1}{2}\)SABC(Vì hai tam giác có chung chiều cao hạ từ đỉnh C xuống đáy AB và BM =\(\dfrac{1}{2}\)AB)
SABC = \(\dfrac{1}{2}\)SABCD(vì ABCD là hình chữ nhật)
⇒ SBMN = \(\dfrac{1}{4}\times\dfrac{1}{2}\times\dfrac{1}{2}\)\(\times\)SABCD = 288 \(\times\)\(\dfrac{1}{16}\) = 18 (cm2)
SMNPQ = SABCD - (SAMQ +SDPQ+SCNP+SBMN)
Diện tích của MNPQ là:
288 - (64 + 24 + 36 + 18) = 146 (cm2)
Đáp số: 146 cm2

A B C D M N P Q
Ta có :
Diện tích tam giác AMQ
\(S_{\Delta AMQ}=\frac{1}{2}.AM.AQ=\frac{1}{2}\frac{1}{2}.AB.\frac{1}{2}AD=\frac{1}{8}.AB.AD=\frac{1}{8}.S_{ABCD}=\frac{1}{8}.216=27\)(cm^2)
Diện tích tam giác BMN
\(S_{\Delta BMN}=\frac{1}{2}.BM.BN=\frac{1}{2}\frac{1}{2}.AB.\frac{2}{3}BC=\frac{1}{6}.AB.BC=\frac{1}{6}.S_{ABCD}=\frac{1}{6}.216=36\)(cm^2)
Diện tích tam giác PNC:
\(S_{\Delta CNP}=\frac{1}{2}.CN.CP=\frac{1}{2}\frac{1}{3}.BC.\frac{2}{3}DC=\frac{1}{9}.BC.CD=\frac{1}{9}.S_{ABCD}=\frac{1}{9}.216=24\)(cm^2)
Diện tích tam giác DPQ:
\(S_{\Delta DPQ}=\frac{1}{2}.DP.DQ=\frac{1}{2}\frac{1}{3}.DC.\frac{1}{2}AD=\frac{1}{12}.DC.AD=\frac{1}{12}.S_{ABCD}=\frac{1}{12}.216=18\)(cm^2)
Diện tích hình MNPQ là:
\(S_{MNPQ}=S_{ABCD}-S_{AQM}-S_{BNM}-S_{CNP}-S_{DPQ}=216-27-36-24-18=111\)(cm^2)
Kết luận:...

SMNPQ = SABCD - SAMQ - SBMN - SCNP - SDPQ
Tính diện tích tam giác AMQ
SABQ / SABD = AQ / AD = 1/3 (hai tam giác chung đường cao hạ từ đỉnh B)
SABQ = SABD x 1/3 ( chú ý: SABD=1/2 SABCD)
SABQ = (216/2 ) x 1/3 = 36 (cm2)
SAMQ / SABQ = AM / AB = 1/3 (hai tam giác chung đường cao hạ từ Q)
SAMQ = SABQ x 1/3
sai đề à bạn
đề đúng đấy chứ , nhưng tôi không biết làm