Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

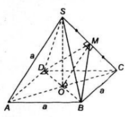
a) Theo giả thiết, S.ABCD là hình chóp đều và đáy ABCD là hình vuông nên SO ⊥ (ABCD) ( tính chất hình chóp đều)
Đáy ABCD là hình vuông cạnh a nên
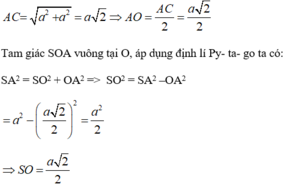

=> Góc giữa hai mặt phẳng (MBD) và (ABCD) là 45 o

s B A D C O M
Hình chiếu vuông góc của SA lên (ABCD) là AO nên góc giữa SA và (ABCD) là \(\widehat{SAO}\)
Xét \(\Delta SAO\left(\perp O\right)\) ta có : \(SA=\frac{a\sqrt{5}}{2};AO=\frac{1}{2}AC=\frac{1}{2}a\sqrt{2}\)
\(\cos\widehat{SAO}=\frac{AO}{SA}=\frac{\frac{a\sqrt{2}}{2}}{\frac{a\sqrt{5}}{2}}=\frac{\sqrt{10}}{5}\)
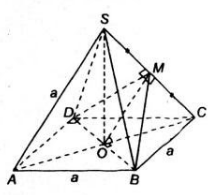
c. Xét \(\Delta SOC\) có : \(\begin{cases}SO\perp BD\\OC\perp BD\end{cases}\) nên \(\left(SOC\right)\perp BD\) mà \(OM\subset\left(SOC\right)\Rightarrow OM\perp BD\)
xét : \(\left(MBD\right)\cap\left(ABCD\right)=BD\)
Trong (MBD) có \(OM\perp BD\)
Trong (ABCD) có \(OC\perp BD\)
Vậy góc giữa (MBD) và (ABCD) là \(\widehat{MOC}\)
Ta có : \(\Delta SAC\) đồng dạng với \(\Delta MOC\) (vì \(CM=\frac{1}{2}CS;CO=\frac{1}{2}CA\))nên \(\widehat{MOC}=\widehat{SAC}\)

Do S.ABCD là chóp đều \(\Rightarrow BD\perp\left(SAC\right)\)
Mà BD là giao tuyến (MBD) và (ABCD)
\(\Rightarrow\widehat{MOC}\) là góc giữa (MBD) và (ABCD)
\(OC=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\) ; \(MC=OM=\dfrac{1}{2}SC=\dfrac{a}{2}\)
Áp dụng định lý hàm cosin:
\(cos\widehat{MOC}=\dfrac{OM^2+OC^2-CM^2}{2OM.OC}=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\widehat{MOC}=45^0\)

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow\widehat{BSC}\) là góc giữa SC và (SAB)
\(tan\widehat{BSC}=\dfrac{BC}{SB}=\dfrac{\sqrt{10}}{5}\Rightarrow SB=\dfrac{a\sqrt{10}}{2}\)
\(\Rightarrow SA=\sqrt{SB^2-AB^2}=\dfrac{a\sqrt{6}}{2}\)
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SOA}\) là góc giữa SO và (ABCD)
\(AO=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\)
\(tan\widehat{SOA}=\dfrac{SA}{AO}=\sqrt{3}\Rightarrow\widehat{SOA}=60^0\)

tham khảo:

a) AB//CD nên góc giữa SC và AB là góc giữa SC và CD: \(\widehat{SCD}\)
cos\(\widehat{SCD}\)=\(\dfrac{\left(2a\right)^2+a^2-\left(2a\right)^2}{2.2a.a}=\dfrac{1}{4}\)
Suy ra \(\widehat{SCD}=75^0\)
b) Kẻ SO⊥(ABCD). Do các cạnh bên của hình chóp bằng nhau nên O là tâm của hình vuông ABCD.
Ta có: AO⊥OB;AC=\(\sqrt{2}.\sqrt{2}\).a=2a;AO=BO=\(\dfrac{1}{2}\).2a=a
Hình chiếu vuông góc của tam giác SAB là tam giác OAB có diện tích là \(\dfrac{1}{2}\).a.a=\(\dfrac{1}{2}.a^2\)


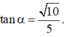




a/ Đề sai
b/ Gọi H là trung điểm OC \(\Rightarrow\) MH là đường trung bình tam giác SOC
\(\Rightarrow MH//SO\Rightarrow MH\perp\left(ABCD\right)\)
Mà \(\left\{{}\begin{matrix}\left(SAC\right)\perp\left(ABCD\right)\\\left(SAC\right)\perp\left(MBD\right)\end{matrix}\right.\) \(\Rightarrow\widehat{MOH}\) là góc giữa (MBD) và (ABCD)
\(AC=a\sqrt{2}\Rightarrow OC=\frac{a\sqrt{2}}{2}\Rightarrow OH=\frac{a\sqrt{2}}{4}\)
\(OM=\frac{1}{2}SC=\frac{a\sqrt{5}}{4}\)
\(\Rightarrow cos\widehat{MOH}=\frac{OH}{OM}=\sqrt{\frac{2}{5}}\Rightarrow\widehat{MOH}\approx50^046'\)
c/ Gọi N là trung điểm AB \(\Rightarrow AB\perp\left(SON\right)\Rightarrow\widehat{SNO}\) là góc giữa (SAB) và (ABCD)
\(ON=\frac{1}{2}BC=\frac{a}{2}\) ; \(SO=\sqrt{SC^2-OC^2}=\frac{a\sqrt{3}}{2}\)
\(tan\widehat{SNO}=\frac{SO}{ON}=\sqrt{3}\Rightarrow\widehat{SNO}=60^0\)