Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

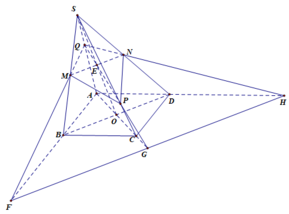
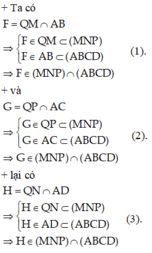
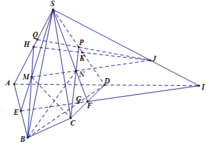
Từ (1) (2) và (3) suy ra ba điểm F, G, H thuộc giao tuyến của hai mặt phẳng (MNP) và (ABCD).
Do đó ba điểm F, G, H thẳng hàng và G nằm giữa F và H.
Chọn C.

Hình câu c là tui vẽ riêng ra cho dễ nhìn thôi, còn hình vẽ trình bày vô bài lấy hình chung ở câu a và b nhó :v



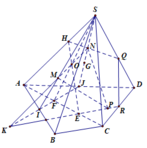
S A B C D O M N P H K
a/
Xét tg SAD có
SM=DM; SN=AN => MN là đường trung bình của tg SAD
=> MN//AD
Mà AD//BC (cạnh đối hbh)
=> MN//BC mà \(BC\in\left(SBC\right)\) => MN//(SBC)
C/m tương tự ta cũng có NP//(SCD)
b/
Ta có
NP//(SCD) (cmt) (1)
Xét tg SBD có
SP=BP (gt)
OB=OD (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
=> PO là đường trung bình của tg SBD
=> PO//SD mà \(SD\in\left(SCD\right)\) => PO//(SCD) (2)
Từ (1) và (2) => (ONP)//(SCD)
C/m tương tự ta cũng có (OMN)//(SBC)
c/
Trong (ABCD) , qua O dựng đường thẳng // AD cắt AB và CD lần lượt tại H và K Ta có
MN//AD (cmt)
=> KH//MN
\(O\in\left(OMN\right);O\in KH\)
\(\Rightarrow KH\in\left(OMN\right)\) mà \(H\in AB;K\in CD\)
=>K; H là giao của (OMN) với CD và AB
d/
Ta có
KH//AD
AB//CD => AH//DK
=> AHKD là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
=> AD=HK
Ta có
MN là đường trung bình của tg SAD (cmt)
\(\Rightarrow MN=\dfrac{AD}{2}\) mà AD=HK (cmt)
\(\Rightarrow MN=\dfrac{HK}{2}\Rightarrow\dfrac{MN}{HK}=\dfrac{1}{2}\)

Đề bài sai òi :v Vẽ hình ra đi bạn.
Giờ tui gán MN vô (SBD) thì giao tuyến của (SBD) và (SBC) là SB. Vậy nên SB phải song song với MN. Nhưng ko :) Song song chết liền hà :)

a/ Một kinh nghiệm khi đề bài cho dữ kiện về trọng tâm thì vẽ hết 3 đường trung tuyến ra, sẽ rất dễ nhìn
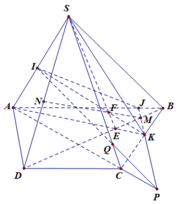
Ta có SG là đường trung tuyến của tam giác SCD, kéo dài SG cắt CD ở K=> \(MG\subset\left(SAK\right)\)
\(\left\{{}\begin{matrix}A\in SA\subset\left(SAK\right)\\A\in AB\subset\left(ABCD\right)\end{matrix}\right.\Rightarrow A=\left(SAK\right)\cap\left(ABCD\right)\)
\(\left\{{}\begin{matrix}K\in SK\subset\left(SAK\right)\\K\in CD\subset\left(ABCD\right)\end{matrix}\right.\Rightarrow K=\left(SAK\right)\cap\left(ABCD\right)\)
\(\Rightarrow\left(SAK\right)\cap\left(ABCD\right)=AK\)
\(AK\cap MG=\left\{I\right\}\Rightarrow MG\cap\left(ABCD\right)=\left\{I\right\}\)
b/ \(BN\subset\left(SBD\right)\)
\(\left(SAG\right)\equiv\left(SAK\right)\)
\(AK\cap BD=\left\{H\right\}\Rightarrow H=\left(SBD\right)\cap\left(SAK\right)\)
\(\Rightarrow\left(SAG\right)\cap\left(SAK\right)=SH\)
\(SH\cap BN=\left\{O\right\}\Rightarrow BN\cap\left(SAG\right)=\left\{O\right\}\)
a/ Một kinh nghiệm khi đề bài cho dữ kiện về trọng tâm thì vẽ hết 3 đường trung tuyến ra, sẽ rất dễ nhìn
Ta có SG là đường trung tuyến của tam giác SCD, kéo dài SG cắt CD ở K=> \(MG\subset\left(SAK\right)\)
\(\left\{{}\begin{matrix}A\in SA\subset\left(SAK\right)\\A\in AB\subset\left(ABCD\right)\end{matrix}\right.\Rightarrow A=\left(SAK\right)\cap\left(ABCD\right)\)
\(\left\{{}\begin{matrix}K\in SK\subset\left(SAK\right)\\K\in CD\subset\left(ABCD\right)\end{matrix}\right.\Rightarrow K=\left(SAK\right)\cap\left(ABCD\right)\)
\(\Rightarrow\left(SAK\right)\cap\left(ABCD\right)=AK\)
\(AK\cap MG=\left\{I\right\}\Rightarrow MG\cap\left(ABCD\right)=\left\{I\right\}\)
b/ \(BN\subset\left(SBD\right)\)
\(\left(SAG\right)\equiv\left(SAK\right)\)
\(AK\cap BD=\left\{H\right\}\Rightarrow H=\left(SBD\right)\cap\left(SAK\right)\)
\(\Rightarrow\left(SAG\right)\cap\left(SAK\right)=SH\)
\(SH\cap BN=\left\{O\right\}\Rightarrow BN\cap\left(SAG\right)=\left\{O\right\}\)