Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
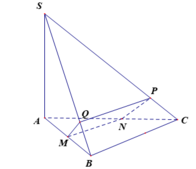
- Trong (SAB), từ M kẻ đường thẳng vuông góc với SB tại Q.
- Trong (SBC) từ Q kẻ đường thẳng vuông góc với SB cắt SC tại P.
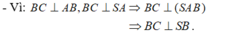
- Do đó BC// QP, trong (ABC) từ M kẻ đường thẳng song song với BC cắt AC tại N.
- Xét tứ giác MNPQ, ta có BC // QP nên tứ giác là là hình thang.
- Mặt khác:
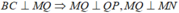
nên tứ giác MNPQ là hình thang vuông.

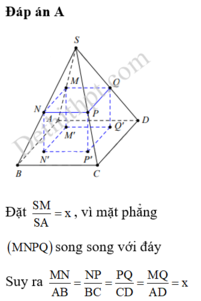
a) () // (ABCD) =>
// AB =>
là trung điểm của SB. Chứng minh tương tự với các điểm còn lại
b) Áp dụng định lí Ta-lét trong không gian:
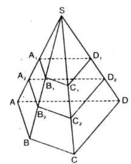
\(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}\).
Do \(A_1A_2=A_2A\) nên : \(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}=1\).
Nên \(B_1B_2=B_2B;C_1C_2=CC_2=D_1D_2=D_2D\).
c) Có hai hình chóp cụt:

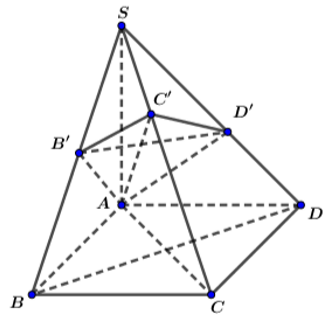
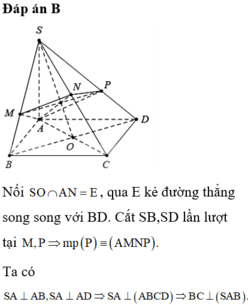
a) Chứng minh B 1 , C 1 , D 1 lần lượt là trung điểm của các cạnh SB, SC, SD
Ta có:
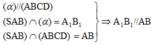
⇒ A 1 B 1 là đường trung bình của tam giác SAB.
⇒ B 1 là trung điểm của SB (đpcm)
*Chứng minh tương tự ta cũng được:
• C 1 là trung điểm của SC.
• D 1 là trung điểm của SD.
b) Chứng minh B 1 B 2 = B 2 B , C 1 C 2 = C 2 C , D 1 D 2 = D 2 D .
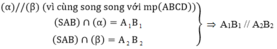
⇒ A 2 B 2 là đường trung bình của hình thang A 1 B 1 B A
⇒ B 2 là trung điểm của B 1 B
⇒ B 1 B 2 = B 2 B (đpcm)
*Chứng minh tương tự ta cũng được:
• C 2 là trung điểm của C 1 C 2 ⇒ C 1 C 2 = C 2 C
• D 2 là trung điểm của D 1 D 2 ⇒ D 1 D 2 = D 2 D .
c) Các hình chóp cụt có một đáy là tứ giác ABCD, đó là : A 1 B 1 C 1 D 1 . A B C D v à A 2 B 2 C 2 D 2 . A B C D




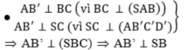



Chọn A.
- Dựng AP ⊥ SD (P ∈ SD).
- Trong mp(SCD) dựng PN ⊥ SD (N ∈ SC)
- Khi đó mặt phẳng (P) ≡ (APN).
- Trong mặt phẳng (ABCD) dựng AK ⊥ AD (K ∈ BC).
- Mà: AK ⊥ SA ⇒ AK ⊥ SD ⇒ K ∈ (APN).
- Trong (SBC) , gọi M = NK ∩ SB. Khi đó tứ giác AMNP là thiết diện của mặt phẳng (P) với hình chóp S.ABCD suy ra tứ giác AMNP nội tiếp đường tròn.
Cách khác:
- Dựng AP ⊥ SD (P ∈ SD).
- Trong (SCD) dựng PN ⊥ SD (N ∈ SC).
- Khi đó mặt phẳng (P) ≡ (APN).
- Trong (ABCD), gọi O = AC ∩ BD.
- Trong (SAC), gọi I = AC ∩ SO.
- Trong (SBD), gọi M = PI ∩ SB.
- Khi đó mặt phẳng (P) ≡ (AMNP).
- Ta có: IA.IN = IP.IM ⇒ AMNP nội tiếp đường tròn.