

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Gọi E là giao điểm của AC và BD \(\Rightarrow\left\{{}\begin{matrix}E\in\left(SAC\right)\\E\in\left(SBD\right)\end{matrix}\right.\)
\(\Rightarrow SE=\left(SAC\right)\cap\left(SBD\right)\)
Kéo dài AD và BC cắt nhau tại F
\(\Rightarrow SF=\left(SAD\right)\cap\left(SBC\right)\)
b.
Chắc là trung điểm của SC và SD?
M và trung điểm SC, N là trung điểm SD
\(\Rightarrow MN\) là đường trung bình tam giác SCD
\(\Rightarrow MN//CD\) , mà \(CD//AB\Rightarrow MN//AB\Rightarrow MN//\left(SAB\right)\)

Mình sẽ tóm tắt và giải từng ý nhé.
Đề cho: Hình chóp S.ABCD, đáy ABCD là tứ giác.
M nằm trong tam giác SBC, N nằm trong tam giác SCD.
a) Giao tuyến của (AMN) và (ABCD)
b) Giao điểm của MN với (SAC)
c) Giao điểm của SC với (AMN)
Tóm lại:
a) AI (I là MN ∩ BD)
b) P = MN ∩ (SAC) (thường là trên SC)
c) Cùng điểm P đó
Nếu bạn muốn mình vẽ hình minh họa để nhìn rõ hơn mình có thể làm ngay.
Cho mình xin 1 tick với ạ

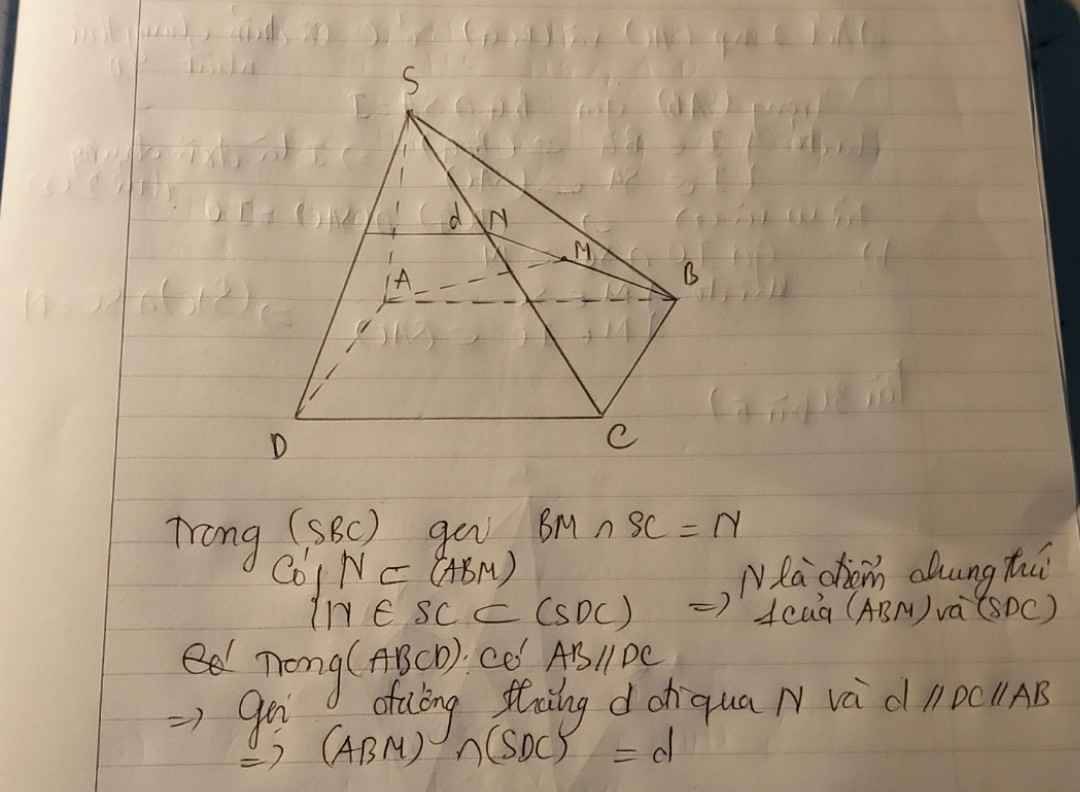
Do AD // BC, M thuộc (SBC) nên giao tuyến của (ADM) với (SBC) là đường thẳng qua M và song song với BC.
Đáp án B