Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a có \(\angle \left(\right. S C , \left(\right. A B C D \left.\right) \left.\right) = 45^{\circ}\).
Nghĩa là hình chiếu của \(S\) xuống đáy nằm trên đường chéo \(B D\).
Xét tam giác cân \(S A B\), do tính đối xứng ⇒ khoảng cách từ \(A\) đến \(\left(\right. S C D \left.\right)\) chính bằng nửa cạnh hình vuông:
\(d\left(\right.A,\left(\right.SCD\left.\right)\left.\right)=\frac{a}{2}\)
Với \(M\) là trung điểm \(S A\), khoảng cách giảm đi một nửa:
\(d\left(\right.M,\left(\right.SCD\left.\right)\left.\right)=\frac{a}{4}\)
Đáp số
\(d \left(\right. A , \left(\right. S C D \left.\right) \left.\right) = \frac{a}{2}\)
\(d \left(\right. M , \left(\right. S C D \left.\right) \left.\right) = \frac{a}{4}\)

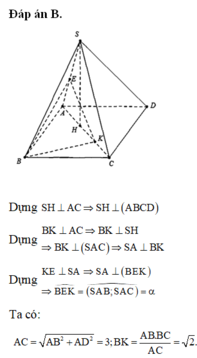
Đáp án B.
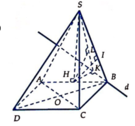
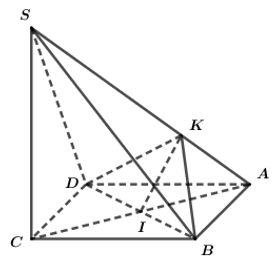
Vẽ đường thẳng d qua B và song song với AC.
Gọi K, I lần lượt là hình chiếu của H trên d và SB, L là hình chiếu của H trên SK.
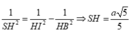
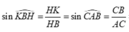
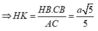
![]()
![]()
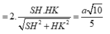
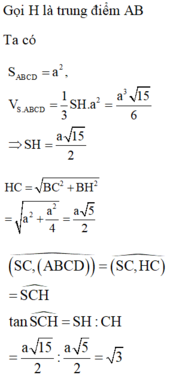

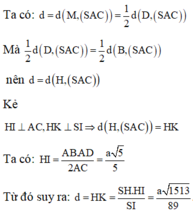





Đáp án A
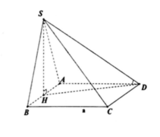
Gọi H là trung điểm của AB, tam giác SAB cân tại S do đó SH⊥AB mà (SAB)⊥ (ABCD) nên SH⊥ (ABCD). Góc giữa SC và đáy là SCH =600.
Tam giác BHC vuông tại B nên
Tam giác SHC vuông tại H nên SH = SC.tanSCH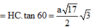
Do vậy