Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho mình hỏi, cái chỗ tính HI không dùng cách này được hả bạn \(\dfrac{SH.HC}{\sqrt{SH^2+HC^2}}\)
Nếu không dùng được, bạn lí giải giùm mình với

a: BC vuông góc SA
BC vuông góc AB
=>CB vuông góc (SBA)
DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
=>(SDC) vuông góc (SAD)
b: (SC;(SAD))=(SC;SD)=góc CSD
\(SD=\sqrt{SA^2+AD^2}=2a\sqrt{7}\)
\(AC=\sqrt{\left(2a\right)^2+3a^2}=a\sqrt{7}\)
\(SC=\sqrt{SA^2+AC^2}=4a\sqrt{2}\)
\(cosCSD=\dfrac{SC^2+SD^2-DC^2}{2\cdot SC\cdot SD}=\dfrac{32a^2+28a^2-4a^2}{2\cdot2a\sqrt{7}\cdot4a\sqrt{2}}=\dfrac{\sqrt{14}}{4}\)
=>góc CSD=21 độ
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=5/căn 7
=>góc SCA=62 độ

Đáp án D
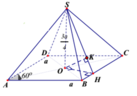
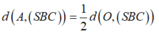
AC cắt (SBC) tại C , O là trung điểm AC =>khoảng cách
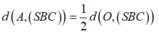
* Trong (ABCD) dựng OH ⊥ BC, trong (SOH) dựng OK ⊥ SH ta chứng minh được OK ⊥ (SBC)
=> khoảng cách d(O,(SBC))= OK.
∆ O B C vuông tại O có OH đường cao
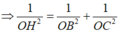
∆ S O H vuông tại O có OK đường cao
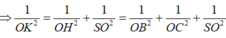
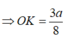
Vậy