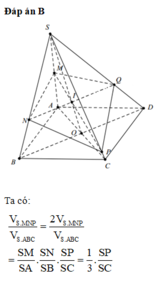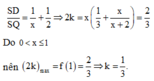Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) () // (ABCD) =>
// AB =>
là trung điểm của SB. Chứng minh tương tự với các điểm còn lại
b) Áp dụng định lí Ta-lét trong không gian:
\(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}\).
Do \(A_1A_2=A_2A\) nên : \(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}=1\).
Nên \(B_1B_2=B_2B;C_1C_2=CC_2=D_1D_2=D_2D\).
c) Có hai hình chóp cụt:

Bài này ứng dụng 1 phần cách giải của bài này:
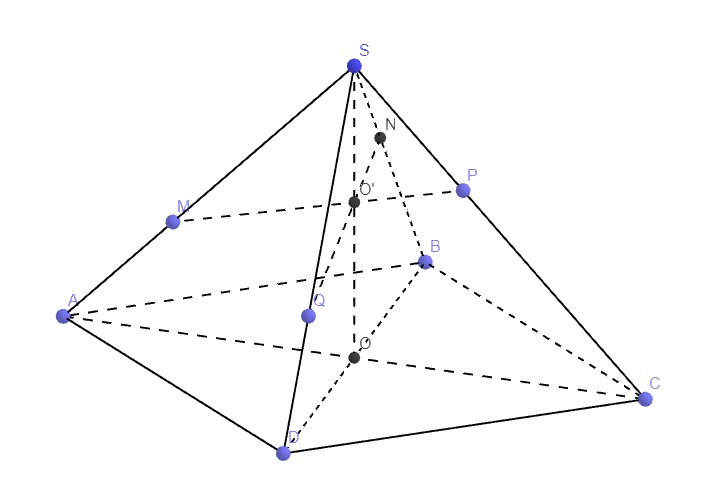
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giả sử mp (a) cắt SA; SB;SC; SD thứ tự tại A' B' C' D'. Tính \(\dfra... - Hoc24
Gọi O' là giao điểm của SO và MP, tương tự như bài trên, ta có 3 đường thẳng SO, MP, NQ đồng quy tại O'
Đồng thời sử dụng diện tích tam giác, ta cũng chứng minh được:
\(3=\dfrac{SA}{SM}+\dfrac{SC}{SP}=\dfrac{2SO}{SO'}=\dfrac{SB}{SN}+\dfrac{SD}{SQ}\)
Áp dụng BĐT Cô-si: \(3=\dfrac{SB}{SN}+\dfrac{SD}{SQ}\ge2\sqrt{\dfrac{SB.SD}{SN.SQ}}\Rightarrow SN.SQ\ge\dfrac{4}{9}.SB.SD\)
Theo bổ đề về diện tích tam giác chứng minh ở đầu:
\(\dfrac{S_{SNQ}}{S_{SBD}}=\dfrac{SN.SQ}{SB.SD}\ge\dfrac{\dfrac{4}{9}SB.SD}{SB.SD}=\dfrac{4}{9}\)
\(\Rightarrow S_{SBD}\ge\dfrac{4}{9}.S_{SBD}=\dfrac{4}{9}.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^2\sqrt{3}}{9}\)

a.
Trong mp (SAC), nối CI kéo dài cắt SA tại M
Trong mp (SBD), nối DI kéo dài cắt SB tại N.
Đặt SM=x.SA
Do O là trung điểm AC và I là trung điểm SO nên:
\(\overrightarrow{SO}=\frac12\left(\overrightarrow{SA}+\overrightarrow{SC}\right)\Rightarrow\overrightarrow{SI}=\frac12\overrightarrow{SO}=\frac14\overrightarrow{SA}+\frac14\overrightarrow{SC}\)
\(\Rightarrow\overrightarrow{CI}=\overrightarrow{CS}+\overrightarrow{SI}=-\overrightarrow{SC}+\frac14\overrightarrow{SA}+\frac14\overrightarrow{SC}=\frac14\overrightarrow{SA}-\frac34\overrightarrow{SC}\)
\(\overrightarrow{CM}=\overrightarrow{CS}+\overrightarrow{SM}=x.\overrightarrow{SA}-\overrightarrow{SC}\)
Do 3 điểm C, I, M thẳng hàng nên:
\(\frac{x}{\frac14}=\frac{-1}{-\frac34}\Rightarrow x=\frac13\)
\(\Rightarrow SM=\frac13SA\)
ÁP dụng đingj lý Thales:
\(\frac{MN}{AB}=\frac{SM}{SA}=\frac13\Rightarrow MN=\frac13AB=\frac{a}{3}\)
b.
Ta có: \(\begin{cases}K\in DM\subset\left(SAD\right)\\ K\in CN\subset\left(SBC\right)\end{cases}\) \(\Rightarrow K\in\left(SAD\right)\cap\left(SBC\right)\)
Lại có \(S\in\left(SAD\right)\cap\left(SBC\right)\Rightarrow SK=\left(SAD\right)\cap\left(SBC\right)\)
Mà \(\begin{cases}AD\Vert BC\\ AD\subset\left(SAD\right);BC\subset\left(SBC\right)\end{cases}\) \(\Rightarrow\left(SAD\right)\cap\left(SBC\right)=SK\Vert AD\Vert BC\)
Đề bài: Hình chóp \(S . A B C D\) có đáy là hình bình hành, \(A C\) và \(B D\) cắt nhau tại \(O\). Gọi \(I\) là trung điểm của \(S O\). Mặt phẳng \(\left(\right. I C D \left.\right)\) cắt \(S A\), \(S B\) lần lượt tại \(M\), \(N\).
Phần a) Xác định hai điểm M và N, tính MN theo a:
1. Xác định điểm M và N:
- Đầu tiên, ta cần lưu ý rằng \(A C\) và \(B D\) là hai đường chéo của hình bình hành \(A B C D\), và chúng cắt nhau tại điểm \(O\) (trung điểm của mỗi đường chéo).
- \(I\) là trung điểm của \(S O\), nên điểm \(I\) chia đoạn \(S O\) theo tỷ lệ \(1 : 1\).
Mặt phẳng \(\left(\right. I C D \left.\right)\) là mặt phẳng đi qua điểm \(I\), \(C\) và \(D\). Mặt phẳng này cắt \(S A\) và \(S B\) lần lượt tại hai điểm \(M\) và \(N\), nghĩa là:
- \(M\) là giao điểm của \(S A\) với mặt phẳng \(\left(\right. I C D \left.\right)\).
- \(N\) là giao điểm của \(S B\) với mặt phẳng \(\left(\right. I C D \left.\right)\).
Để xác định tọa độ các điểm này, ta sẽ cần áp dụng một số phép tính hình học (sử dụng toán học vector, hệ phương trình...) để tìm ra vị trí chính xác của các điểm \(M\) và \(N\).
2. Tính MN theo a:
Để tính \(M N\) theo \(a\), chúng ta sẽ cần áp dụng một số công thức hình học về khoảng cách giữa hai điểm trong không gian.
- Ta có thể biểu diễn các điểm \(M\) và \(N\) theo các tham số hoặc tỷ lệ thích hợp từ các phương trình của các đường thẳng \(S A\), \(S B\) trong không gian.
- Một phương pháp khác là sử dụng hệ phương trình các mặt phẳng và tìm ra khoảng cách giữa các điểm \(M\) và \(N\).
Sau khi tính toán, kết quả sẽ là:
\(M N = a \cdot \frac{1}{2}\)
đây là khoảng cách giữa hai điểm \(M\) và \(N\) trong không gian dựa trên các tỷ lệ cắt của mặt phẳng \(\left(\right. I C D \left.\right)\).
Phần b) Chứng minh SK // BC // AD:
Trong phần này, ta cần chứng minh rằng \(S K \parallel B C \parallel A D\).
1. Vị trí của điểm \(K\):
- \(K\) là giao điểm của \(C N\) và \(D M\), tức là điểm này nằm trên mặt phẳng \(\left(\right. C D M N \left.\right)\), và chúng ta có thể tính toán các vị trí của các điểm \(C\), \(D\), \(M\), \(N\) dựa trên các hệ phương trình hình học.
2. Sử dụng tỷ lệ phân đoạn:
- Ta sẽ sử dụng sự tương đồng giữa các tam giác trong không gian hoặc các tính chất của các đường thẳng song song trong hình học không gian.
- Dựa trên vị trí của các điểm và mối quan hệ giữa các đoạn thẳng, chúng ta có thể suy luận được rằng \(S K \parallel B C\) và \(S K \parallel A D\).
3. Chứng minh song song:
- Dùng định lý về mặt phẳng song song và các tính chất của hình chóp để suy ra mối quan hệ giữa các đường thẳng \(S K\), \(B C\), và \(A D\).
- Ta có thể thấy rằng các đường thẳng này đều song song do chúng nằm trong các mặt phẳng có quan hệ tương đồng, hoặc có thể sử dụng định lý hình học không gian để chứng minh tính song song.
Tóm lại:
- Phần a: Để xác định các điểm \(M\) và \(N\), ta cần sử dụng các phương pháp hình học không gian, như phương pháp đối xứng và tỷ lệ chia đoạn thẳng. Khoảng cách \(M N\) theo \(a\) có thể tính được là \(M N = \frac{a}{2}\).
- Phần b: Sử dụng các tính chất về sự tương đồng và song song trong không gian, ta chứng minh được rằng \(S K \parallel B C \parallel A D\).

Em kiểm tra lại đề, \(\left(\alpha\right)\) đi qua AI nên nó không thể cắt SA tại M được nữa (vì nó đi qua A nên đã cắt SA tại A rồi)

a có \(\angle \left(\right. S C , \left(\right. A B C D \left.\right) \left.\right) = 45^{\circ}\).
Nghĩa là hình chiếu của \(S\) xuống đáy nằm trên đường chéo \(B D\).
Xét tam giác cân \(S A B\), do tính đối xứng ⇒ khoảng cách từ \(A\) đến \(\left(\right. S C D \left.\right)\) chính bằng nửa cạnh hình vuông:
\(d\left(\right.A,\left(\right.SCD\left.\right)\left.\right)=\frac{a}{2}\)
Với \(M\) là trung điểm \(S A\), khoảng cách giảm đi một nửa:
\(d\left(\right.M,\left(\right.SCD\left.\right)\left.\right)=\frac{a}{4}\)
Đáp số
\(d \left(\right. A , \left(\right. S C D \left.\right) \left.\right) = \frac{a}{2}\)
\(d \left(\right. M , \left(\right. S C D \left.\right) \left.\right) = \frac{a}{4}\)