Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha
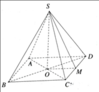
a, Gọi \(O=BD\cap AC\)
K là trung điểm của CD
\(\Rightarrow OK=\dfrac{1}{2}AD=\dfrac{1}{2}CD=5\)
b, \(S_{xq}=\left(AB+BC\right).SK\)
\(=\left(10+10\right).13\)
\(=260\left(cm^2\right)\)
c, \(V_{S_{ABCD}}=\dfrac{1}{3}.SO.SB.SC\)
\(=\dfrac{1}{3}.12.10.10\)
\(=400\left(cm^3\right)\)
-Chúc bạn học tốt-

Hình chóp tam giác đều nên là chiều cao của mặt bên xuất phát từ đỉnh chính là trung đoạn
Sxq=1/2*10*3*12=5*36=180cm2

a) Diện tích xung quanh của hình chóp tam giác đều là: \(\frac{{10.3}}{2}.12 = 180\) (\(c{m^2}\))
b) Diện tích xung quanh của hình chóp tứ giác đều là: \(\frac{{72.4}}{2}.77 = 11088\) (\(d{m^2}\))
Diện tích đáy của hình chóp tứ giác đều là: \({72^2}=5184\) (\(d{m^2}\))
Diện tích toàn phần của hình chóp tứ giác đều là: \(11088 + 5184 = 16 272\) (\(d{m^2}\))
Thể tích của hình chóp tứ giác đều là: \(\frac{1}{3}.5184.68,1=117676,8\) (\(d{m^3}\))

Lời giải:
Xét tam giác $SAB$ có $SA=SB=10$, $AB=12$
Kẻ $SH\perp AB$ thì $H$ là trung điểm của $AB$.
$\Rightarrow AH=6$ (cm)
Theo định lý Pitago:
$SH=\sqrt{SA^2-AH^2}=\sqrt{10^2-6^2}=8$ (cm)
$S_{SAB}=\frac{SH.AB}{2}=\frac{8.12}{2}=48$ (cm vuông)
$S_{xq}=3S_{SAB}=3.48=144$ (cm vuông)

Chu vi đáy là:
8*4=32(cm)
Diện tích xung quanh là:
\(32\cdot10=320\left(cm^2\right)\)