Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

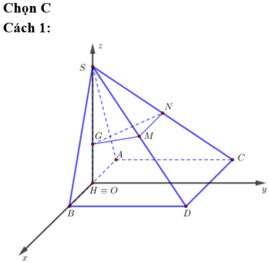
Chọn hệ trục tọa độ Oxyz như hình vẽ. Khi đó
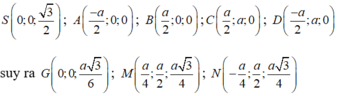
Ta có mặt phẳng (ABCD) có vectơ pháp tuyến là ![]() , mặt phẳng (GMN) có vectơ pháp tuyến là
, mặt phẳng (GMN) có vectơ pháp tuyến là 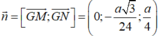
Gọi (α) là góc giữa hai mặt phẳng (GMN) và (ABCD), ta có
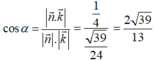
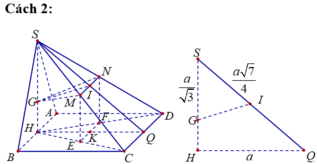
Gọi E, F lần lượt là hình chiếu của M và N lên (ABCD). Suy ra E, F lần lượt là trung điểm của HC, HD.
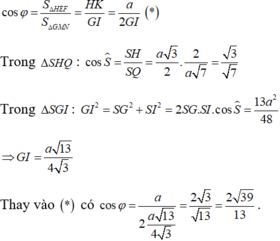
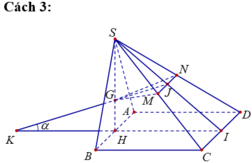
Gọi H, I lần lượt là trung điểm của AB, CD.
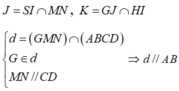
Mà d ⊥ (SIH) nên góc giữa góc giữa hai mặt phẳng (GMN) và (ABCD) là ![]()
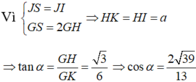

Đáp án D
Hướng dẫn giải:
Ta có S A B C = a 2 2 , S A = S B 2 - A B 2 = a 3
V S . A B C = 1 3 S A . S A B C = 1 3 a 3 . a 2 2 = a 3 3 6
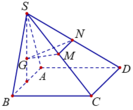
Ta lại có V B . N A M V B . C A S = B N B C . B M B S = 1 4
⇒ V B . N A M = 1 4 V B . C A S
Kết luận V A . S C N M = V S . A B C - V B . N A M = a 3 3 8

Chọn A.
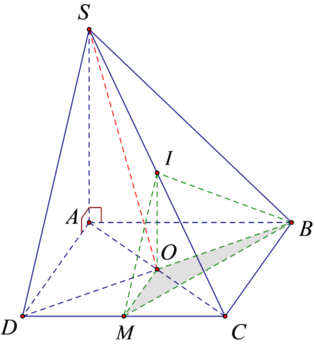
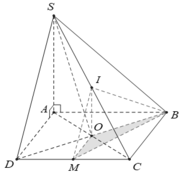
Do IO là đường trung bình của tam giác SAC nên:
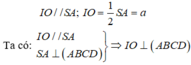
* OM là đường trung bình tam giác ACD nên:
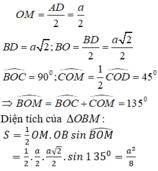
Tính thể tích của khối chóp I.OBM:
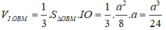

Chọn đáp án C
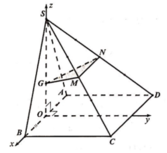
Gọi O là trung điểm AB.
Do tam giác SAB đều và nằm trong mặt phẳng vuông góc (ABCD) nên![]()
Chọn hệ trục tọa độ Oxyz như hình vẽ. Chọn a = 2.
Khi đó: ![]()
![]()
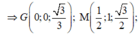
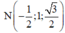
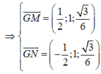
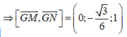
Ta có mặt phẳng (ABCD) có vecto pháp tuyến là ![]()
Mặt phẳng (GMN) có vecto pháp tuyến là 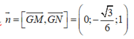
Gọi α là góc giữa hai mặt phẳng (GMN) và (ABCD)
Ta có:
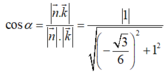


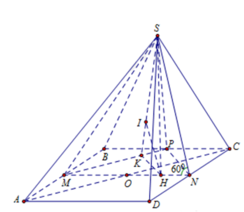



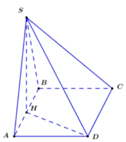
Dựng hình như hình vẽ (E, P, Q, N lần lượt là trung điểm các cạnh)
\(MN||AB\Rightarrow N\in\left(MCD\right)\)
F là giao điểm MN và SE \(\Rightarrow\) F cũng là trung điểm SE
Do tính đối xứng của chóp đều \(\Rightarrow MP=NP\Rightarrow PF\perp MN\) (trung tuyến đồng thời là đường cao)
\(\Rightarrow PF\perp\left(SAB\right)\) (do MN là giao tuyến của 2 mp vuông góc)
\(\Rightarrow PF\perp SE\Rightarrow\Delta SEP\) cân tại P (PF là trung tuyến kiêm đường cao)
\(\Rightarrow\Delta SEP\) đều (do chóp đều nên SEP cũng cân tại S)
\(\Rightarrow SO=a\sqrt{3}\)
MN song song và bằng 1/2 AB (đường trung bình)
OQ song song và bằng 1/2 AB (hiển nhiên)
\(\Rightarrow MNQO\) là hbh \(\Rightarrow OM||NQ\Rightarrow OM||\left(SBC\right)\)
\(\Rightarrow d\left(OM;SB\right)=d\left(OM;\left(SBC\right)\right)=d\left(O;\left(SBC\right)\right)\)
Từ O kẻ \(OH\perp SQ\Rightarrow OH=d\left(O;\left(SBC\right)\right)\)
\(\dfrac{1}{OH^2}=\dfrac{1}{OQ^2}+\dfrac{1}{SO^2}=\dfrac{1}{a^2}+\dfrac{1}{3a^2}\Rightarrow OH\)
@Nguyễn Việt Lâm ơi đại ca giúp em với