Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
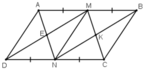
ABCD là hình bình hành ⇒ AB = CD.
M là trung điểm AB ⇒ AM = MB = AB/2.
N là trung điểm CD ⇒ CN = DN = CD/2.
⇒ AM = MB = CN = DN.
+ Tứ giác BMDN có: BM // DN và BM = DN
⇒ BMDN là hình bình hành
⇒ DM // BN hay ME // NK
+ Tứ giác AMCN có: AM // NC, AM = NC
⇒ AMCN là hình bình hành
⇒ AN // CM hay EN // MK.
+ Tứ giác MENK có: ME // NK và NE // MK
⇒ MENK là hình bình hành.
a) MENK là hình thoi
⇔ MN ⊥ EK.
⇔ CD ⊥ AD (Vì EK // CD và MN // AD)
⇔ ABCD là hình chữ nhật.
b) MENK là hình chữ nhật
⇔ MN = EK
Mà MN = BC;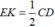 
(vì tam giác MCD có E và K lần lượt là trung điểm MD, MC nên EK là đường trung bình của tam giác MCD).
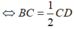
⇔ CD = 2.BC.
c) MENK là hình vuông
⇔ MENK là hình thoi và đồng thời là hình chữ nhật
⇔ ABCD là hình chữ nhật và có CD = 2.BC.
1: Xét tứ giác AMND có
AM//ND
AM=ND
Do đó: AMND là hình bình hành
Suy ra: Hai đường chéo AN cắt MD tại trung điểm của mỗi đường
=>K là trung điểm chung của AN và MD
Xét tứ giác MBCN có
MB//CN
MB=CN
Do đó: MBCN là hình bình hành
Suy ra: Hai đường chéo MC và BN cắt nhau tại trung điểm của mỗi đường
=>L là trung điểm chung của BN và CM
2: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
Suy ra: Hai đường chéo AC và MN cắt nhau tại trung điểm của mỗi đường(1)
Xét tứ giác MKNL có
MK//NL
ML//NK
Do đó: MKNL là hình bình hành
Suy ra: Hai đường chéo MN và KL cắt nhau tại trung điểm của mỗi đường(2)
Ta có: ABCD là hình bình hành
nên Hai đườg chéo AC và BD cắt nhau tại trung điểm của mỗi đường(3)
Từ (1), (2) và (3) suy ra AC,BD,MN,KL đồng quy
Tự vẽ hình nha
a) Vì M là trung điểm AB, N là trung điểm CD
=> MN là đường trung bình
=> MN // AD // BC
và MN = ( AD + BC ) : 2 = AD = BC ( vì ABCD là hình thoi nên AD = BC )
Xét tứ giác AMND có MN // AD và MN = AD
=> AMND là hình bình hành ( đpcm )
b) Vì MN // BC và MN = BC
=> BMNC là hình bình hành
=> hai đường chéo BN và CM cắt nhau tại L là trung điểm mỗi đường ( đpcm )
c) Xét tam giác DAM và tam giác BCN có
AD = BC
góc DAM = góc BCN ( trong hình thoi và hình bình hành, hai góc đối bằng nhau )
AM = CN = ( AB/2 = DC/2 do AB = DC )
=> tam giác DMA = tam giác BNC ( c-g-c )
=> góc AMD = góc BNC ( c g t ư )
Có AB // DC
=> góc AMD = góc MDN ( cặp góc so le trong )
mà góc AMD = góc BNC
=> góc BNC = góc MDN
mà hai góc này đồng vị
=> MD // BN
mà MB // DN ( AB // CD )
=> MBND là hình bình hành
=> BD cắt MN tại trung điểm O của MN
Chứng minh tương tự với hình AMCN
=> AC cắt MN tại trung điểm O của MN
Vì M là trung điểm AB, L là trung điểm BN
=> ML là đường trung bình trong tam giác BAN
=> ML // AN
và ML = 1/2 AN = AK ( AMND là hình bình hành, K là giao hai đường chéo nên K là trung điểm AN )
Xét tứ giác MLNK có ML // KN, ML = KN
=> MLKN là hình bình hành
=> MN giao KL tại trung điểm O của MN
Vì bốn đường thẳng AC, BD, MN , KL cùng đi qua O
=> chúng đồng quy ( đpcm )