Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình.
a, \(xy\) cách \(\left(O\right)\) một khoảng \(OK=a\)
Mà \(OK< R\)
=> \(K\in xy\) và \(xy\) cắt \(\left(O\right)\) tại hai điểm D và E
b, \(OK\perp xy\) đồng thời \(OK\perp AK\) => \(\widehat{AKO}=90^o\) => K thuộc đường tròn đường kính AO (1)
AC, AB là 2 tiếp tuyến => \(\hept{\begin{cases}AC\perp CO\\AB\perp BO\end{cases}}\)=> \(\hept{\begin{cases}\widehat{ACO}=90^o\\\widehat{ABO}=90^o\end{cases}}\)
=> B, C thuộc đường kính BC (2)
(1); (2) => K, B, C thuộc đường kính BC
Hay O, A, B, C, K cùng thuộc đường kính BC
c, \(AK\perp KO\)
=> \(\widehat{AKS}=90^o\)
=> K thuộc đường tròn đường kính AS (3)
=> \(AO\perp BC\) tại M
=> \(\widehat{AMS}=90^o\)
=> M thuộc đường tròn đường kính AS (4)
(3); (4) => AMKS nội tiếp

A B M C N D O E
a) Ta có : \(\widehat{ANC}=\widehat{ACM}=\frac{1}{2}\) sđ cung MC ; Góc CAN là góc chung của hai tam giác CAM và tam giác NAC
\(\Rightarrow\Delta CAM~\Delta NAC\left(g.g\right)\) \(\Rightarrow\frac{CM}{CN}=\frac{AC}{AN}\) (1)
Tương tự với tam giác BAM và tam giác NAB ta cũng có \(\widehat{MBA}=\widehat{ANB}=\frac{1}{2}\)sđ cung BM ; Góc NAB là góc chung của hai tam giác
\(\Rightarrow\Delta BAM~\Delta NAB\left(g.g\right)\Rightarrow\frac{AB}{AN}=\frac{BM}{BN}\) (2)
Mà AB = AC (vì AB và AB là hai tiếp tuyến của (O))
Do đó, kết hợp (1) và (2) ta có \(\frac{CM}{CN}=\frac{BM}{BN}\Rightarrow BM.CN=BN.CM\)
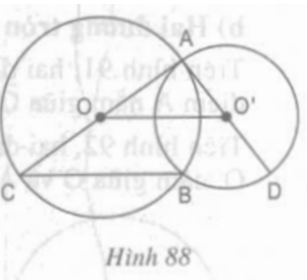
a) Hai đường tròn (O) và (O’) cắt nhau
b) Xét tam giác ABC có:
OA = OB = OC = bán kính đường tròn (O)
Mà BO là trung tuyến của tam giác ABC
⇒ ∆ABC vuông tại B ⇒ AB ⊥ BC (1)
Lại có OO’ là đường trung trực của AB
⇒ AB ⊥ OO' (2)
Từ (1) và (2) ⇒ OO’ // BC
Chứng minh tương tự ta có ∆ABD vuông tại B ⇒ AB ⊥ BD (3)
Từ (1) và (3) ⇒ B, C, D thẳng hàng.