Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
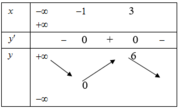
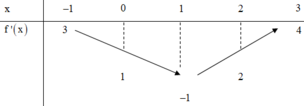
Dựa vào bảng biến thiên suy ra hàm số nghịch biến trên (0;1)

Tập xác định : D = [0 ; 2]; y' = , ∀x ∈ (0 ; 2); y' = 0 ⇔ x = 1.
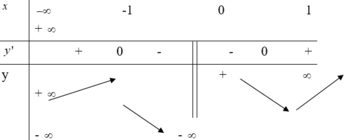
Bảng biến thiên :
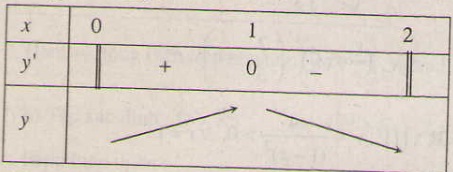
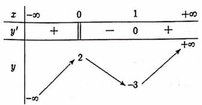
Vậy hàm số đồng biến trên khoảng (0 ; 1) và nghịch biến trên khoảng (1 ; 2).

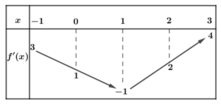
Có y ' = 0 ⇔ [ - 1 < x < 0 0 < x < 1
Đối chiếu các đáp án chọn A.
Chọn đáp án A.

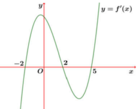
Ta có ![]()
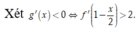
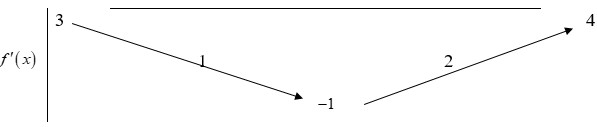
= TH1: ![]() Do đó hàm số nghịch biến trên (-4;-2)
Do đó hàm số nghịch biến trên (-4;-2)
= TH2: ![]() nên hàm số chỉ nghịch biến trên khoảng (2-2a;4) chứ không nghịch biến trên toàn khoảng (2;4)
nên hàm số chỉ nghịch biến trên khoảng (2-2a;4) chứ không nghịch biến trên toàn khoảng (2;4)
Vậy hàm số 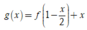 nghịch biến trên (-4;-2)
nghịch biến trên (-4;-2)
Chọn A.

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

Tập xác định : D = R. y' = => y' = 0 ⇔ x=-1 hoặc x=1.
Bảng biến thiên :
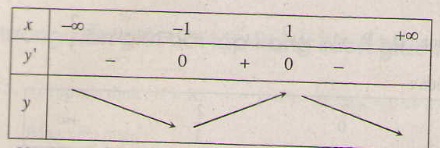
Vậy hàm số đồng biến trên khoảng (-1 ; 1); nghịch biến trên các khoảng (-∞ ; -1), (1 ; +∞).




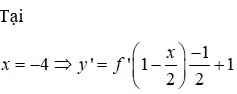
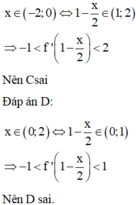
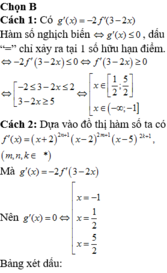
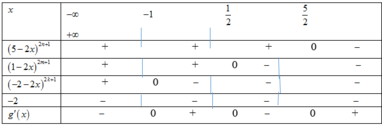
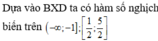
Chọn D