Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vẽ đồ thị
b) Gọi yA, yB, yC lần lượt là tung độ các điểm A, B, C có cùng hoành độ x = -1,5. Ta có:
yA = . (-1,5)2 =
. 2,25 = 1,125
yB = (-1,5)2 = 2,25
yC = 2 (-1,5)2 = 2 . 2,25 = 4,5
c) Gọi yA, yB, yC’ lần lượt là tung độ các điểm A', B', C' có cùng hoành độ x = 1,5. Ta có:
yA, = . 1,52 =
. 2,25 = 1,125
yB, = 1,52 = 2,25
yC’ = 2 . 1,52 = 2 . 2,25 = 4,5
Kiểm tra tính đối xứng: A và A', B và B', C và C' đối xứng với nhau qua trục tung Oy.
d) Với mỗi hàm số đã cho ta đều có hệ số a > 0 nên O là điểm thấp nhất của đồ thị. Khi đó ta có x = 0.
Vậy x = 0 thì hàm số có giả trị nhỏ nhất.

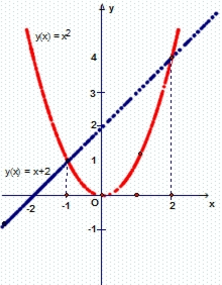
a) (P) là parabol đi qua gốc toạ độ O(0; 0) ; điểm (1; 1/2) và điểm (-1;1/2)
b) A \(\in\) (P) => yA = \(\frac{1}{2}\). xA2 = \(\frac{1}{2}\). (-1)2 = \(\frac{1}{2}\)=> A (-1; \(\frac{1}{2}\))
B \(\in\) (P) => yB = \(\frac{1}{2}\).xB2 = \(\frac{1}{2}\).4 = 2 => B (2; 2)
+) đường thẳng có hệ số góc bằng \(\frac{1}{2}\) có dạng y = \(\frac{1}{2}\)x + b (d)
A \(\in\) d => yA = \(\frac{1}{2}\).xA + b => \(\frac{1}{2}\) = \(\frac{1}{2}\). (-1) + b => b = 1
Vậy đường thẳng (d) có dạng y = \(\frac{1}{2}\)x + 1
Nhận xét: yB = \(\frac{1}{2}\).xB + 1 => B \(\in\) (d)

Nếu quá dài ko trả lời hết thì các p cki cần làm nhanh giúp mk câu : 1.8 ; 2.2 đến 2.5 và 3.2 đến 3.7 thôi cũng dk . mk thật lòng biết ơn .
Câu 1.1:
Nghiệm lớn nhất của phương trình x4 - 29x2 + 100 = 0 là x = ...........phương trình này vô nghiệm nhé
Câu 1.3:
Một hình trụ có diện tích xung quanh là 80π cm2 và thể tích là 160π cm2.
Bán kính đáy của hình trụ này là R = .......4.... cm.
Câu 1.4:
Khi phương trình x2 - 3x + m = 0 có một nghiệm là x = 1,25 thì nghiệm còn lại của phương trình là x = ........1,75.......
Câu 1.8:
Hai tổ cùng làm chung một công việc trong 12 giờ thì xong. Nhưng hai tổ cùng làm trong 4 giờ thì tổ 1 đi làm việc khác, tổ 2 làm nốt trong 10 giờ mới xong việc. Nếu làm riêng thì tổ 2 mất .....60.. giờ sẽ xong việc.
Câu 1.9
Nghiệm nguyên của phương trình: x4 + 5x3 - 12x2 + 5x + 1 = 0 là x = .....1.......
Câu 1.10:
Nghiệm âm của phương trình (x2 + 3x + 2)(x2 + 7x + 12) = 120 là x = ...1.......
Bài 2: Đi tìm kho báu
Câu 2.2:
Nghiệm nguyên của phương trình: 2x4 - 3x3 - 7x2 + 12x = 4 là .....1......
Câu 2.3:
Cho tam giác ABC vuông cân tại A. Trên nửa mặt phẳng bờ BC không chứa điểm A vẽ tam giác cân BCD có góc CBD = 90o. Biết độ dài cạnh AC = 3√5cm.
Độ dài đoạn AD = .....Căn 6...... cm.
Câu 2.4:
Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): y = mx + m - 1.
Giá trị m nguyên để (d) tạo với 2 trục tọa độ tam giác có diện tích 2 (đvdt) là ....1.......
Câu 2.5:
Cho a, b, c > 0 thỏa mãn a + b + c = 1.
Giá trị nhỏ nhất của biểu thức A = bc/a + ca/b + ab/c bằng ......3.....
Bài 3: Đỉnh núi trí tuệ
Câu 3.1:
Cho đường tròn (O; 13cm). Biết khoảng cách từ tâm O đến dây PQ bằng 5cm.
Độ dài dây PQ = .....24......cm.
Câu 3.2:
Cho hàm số y = 1/2 .x2 có đồ thi là (P).
Trên (P) lấy hai điểm A, B có hoành độ lần lượt là -1; 2.
Phương trình đường thẳng AB có tung độ gốc là .......2.....
Câu 3.3:
Phương trình x2 - 2(m + 2)x + 2m - 1 = 0 có hai nghiệm là độ dài hai cạnh góc vuông của một tam giác vuông có cạnh huyền bằng √34.
Khi đó m = ...Chịu........
Câu 3.4:
Một đa giác có số đường chéo nhiều hơn số cạnh là 12. Số cạnh của đa giác là ...8.......
Câu 3.5:
Cho parabol (P): y = ax2 và đường thẳng (d) có hệ số góc bằng 2. Biết (d) và (P) có một điểm chung duy nhất là A có hoành độ bằng 2. Khi đó tung độ của điểm A là ...Chịu.........
Câu 3.6:
Cho phương trình x2 - 5x - 1 = 0 có các nghiệm x1, x2. Biểu thức B = (x13 - 5x12 + 2)(x23 - 5x22 + 2) có giá trị là ......Chịu.....
Câu 3.7:
Cho a, b > 0 và 3a + 5b = 12.
Giá trị lớn nhất của biểu thức P = ab là ...Chịu nốt........
Nhập kết quả dưới dạng phân số tối giản.

a. Vẽ được rồi nên thôi
Hai điểm A(-2, 2) và B(1, 1/2)
b. Đường thẳng AB có PT: x + 2y - 2 = 0.
c. Diện tích tam giác ABC = \(\frac{1}{2}\)AB x d(C/AB)
AB cố định. => Diện tích tam giác ABC lớn nhất khi d(C/AB) lớn nhất
Điểm C có tọa độ (x; \(\frac{x^2}{2}\))
d(C/AB) = \(\frac{\left|x+2\frac{x^2}{2}-2\right|}{\sqrt{1^2+2^2}}\)
d(C/AB) đạt max khi \(\left|x+x^2-2\right|\) đạt max (vì C thuộc cung AB nên -2 < x < 1)
Ta có x2 + x - 2 = (x + 2)(x - 1)
với -2 < x < 1 => x2 + x - 2 < 0
=> \(\left|x^2+x-2\right|\)= -x2 - x + 2 (khi 2- < x < 1)
Vậy, d(C/AB) đạt max khi -x2 - x + 2 đạt max (khi 2- < x < 1)
-x2 -x + 2 = -(x + \(\frac{1}{2}\))2 + \(\frac{1}{4}\) + 2
= -(x +\(\frac{1}{2}\))2 + 9/4 >= 9/4
Vậy, d(C/AB) đạt max khi x = -\(\frac{1}{2}\)
Thay x = \(-\frac{1}{2}\)vào (P): y = \(\frac{x^2}{2}\)
Vậy, Điểm C: (\(-\frac{1}{2}\); \(\frac{1}{8}\))