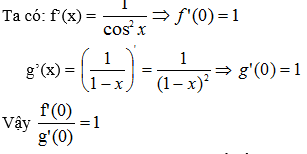K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MH
9 tháng 4 2017
a) ∆y = f(x+∆x) - f(x) = 2(x+∆x) - 5 - (2x - 5) = 2∆x và =
= 2.
b) ∆y = f(x+∆x) - f(x) = (X+ ∆x)2 - 1 - (x2 - 1) = 2x∆x + (∆x)2 = ∆x(2x + ∆x) và =
= 2x + ∆x.
c) ∆y = f(x+∆x) - f(x) = 2(x + ∆x)3 - 2x3 = 6x2∆x + 6x(∆x)2 + 2(∆x)3 = 2∆x.(3x2 + 3x∆x + (∆x)2 ) và = 6x2 + 6x∆x + 2(∆x)2.
d) ∆y = f(x+∆x) - f(x) = -
= -
và
=
.
14 tháng 5 2022
Tham khảo:
Xét hàm số g(x) = f(x) − f(x + 0,5)
Ta có
g(0) = f(0) − f(0 + 0,5) = f(0) − f(0,5)
g(0,5) = f(0,5) − f(0,5 + 0,5) = f(0,5) − f(1) = f(0,5) − f(0)
(vì theo giả thiết f(0) = f(1)).
Do đó,
