K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BT
14 tháng 4 2017
\(\lim\limits_{x\rightarrow0}\left|f\left(x\right)\right|=\lim\limits_{x\rightarrow0}\left|x^2sin\dfrac{1}{x}\right|< \lim\limits_{x\rightarrow0}\left|x^2\right|=0\).
Vậy \(\lim\limits_{x\rightarrow0}f\left(x\right)=0\).
\(f\left(0\right)=A\).
Để hàm số liên tục tại \(x=0\) thì \(\lim\limits_{x\rightarrow0}f\left(x\right)=f\left(0\right)\Leftrightarrow A=0\).
Để xét hàm số có đạo hàm tại \(x=0\) ta xét giới hạn:
\(\lim\limits_{x\rightarrow0}\dfrac{f\left(x\right)-f\left(0\right)}{x-0}=\lim\limits_{x\rightarrow0}\dfrac{x^2sin\dfrac{1}{x}}{x}=\lim\limits_{x\rightarrow0}xsin\dfrac{1}{x}=0\).
Vậy hàm số có đạo hàm tại \(x=0\).
Đáp án D
- Phương pháp: Sử dụng công thức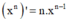
và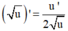 
tính f'(x). Từ đó giải bất phương trình.
- Cách giải:
+ Ta có: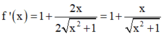
+ Theo đề bài ta có: 2x.f'(x) - f(x) ≥ 0.
+ Thử các đáp án:
+ Với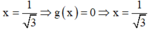
thuộc tập nghiệm của BPT.
⇒ Loại đáp án A, B và C.