Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


( Mình sẽ làm tắt nha bạn, mấy chỗ đấy nó dễ rùi nếu ko hiểu thì cmt nhé )
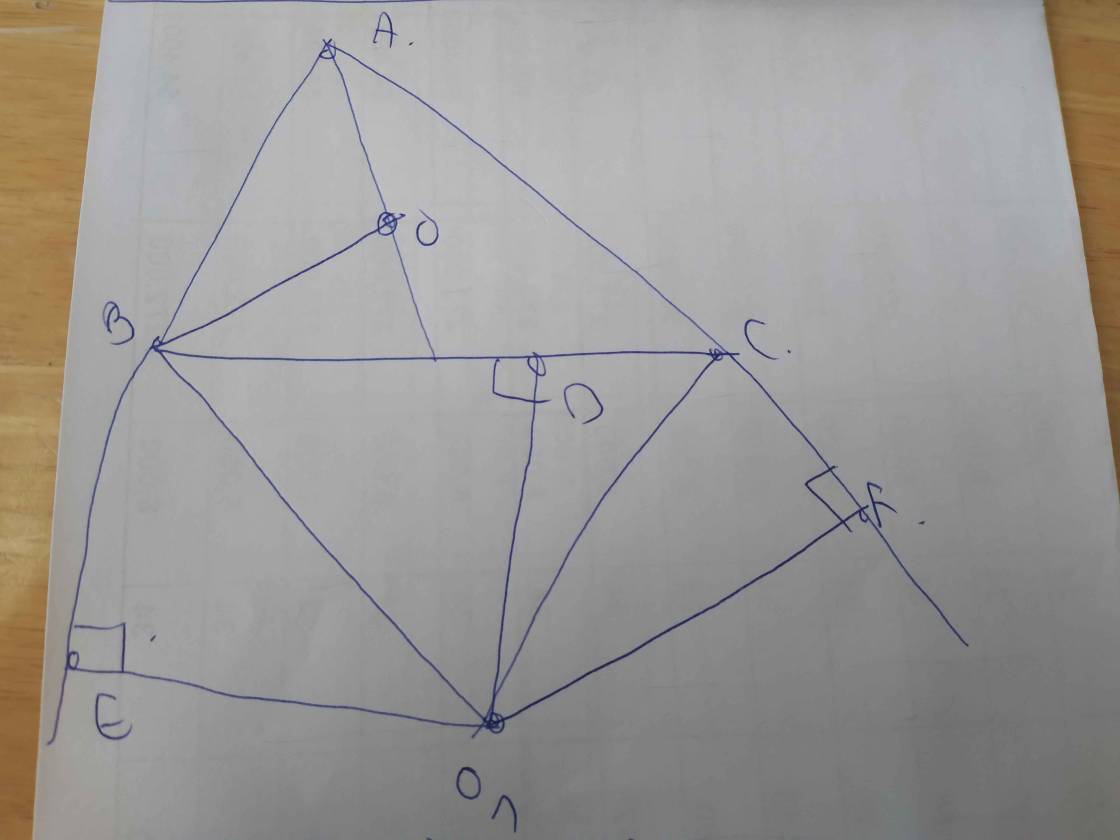
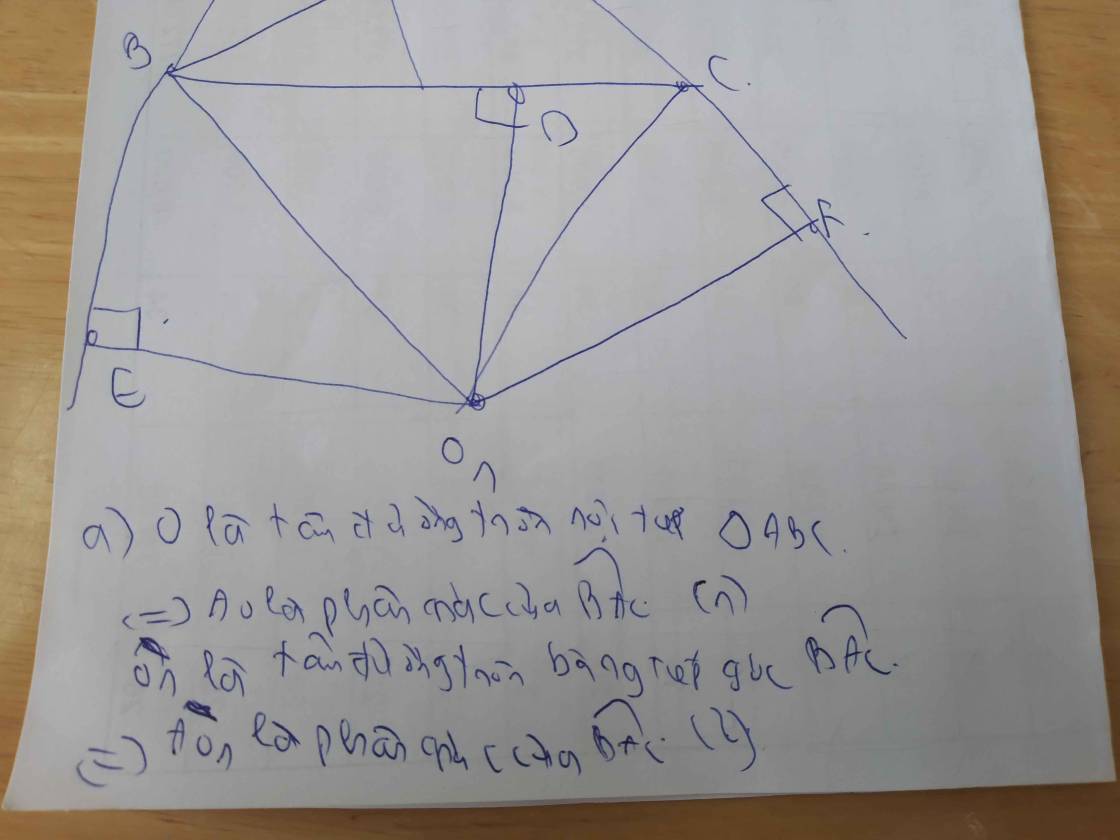
a) Ta có: \(O_1B//O_2C\)( cùng vuông góc với BC )
\(\Rightarrow\widehat{BO_1A}+\widehat{CO_2A}=180^0\)
\(\Leftrightarrow\left(180^0-2\widehat{BAO_1}\right)+\left(180^0-2\widehat{CAO_2}\right)=180^0\)
\(\Leftrightarrow2\left(\widehat{BAO_1}+\widehat{CAO_2}\right)=180^0\)
\(\Leftrightarrow\widehat{BAO_1}+\widehat{CAO_2}=90^0\)
\(\Rightarrow\widehat{BAC}=90^0\)
=> tam giác ABC vuông tại A
b) \(\widehat{O_1BA}+\widehat{MBA}=\widehat{O_1AB}+\widehat{BAM}=90^0\)
\(\Rightarrow\widehat{O_1AM}=90^0\)
\(\Rightarrow AM\perp AO_1\)
=> AM là tiếp tuyến của \(\left(O_1\right)\)
CMTT : AM là tiếp tuyến của \(\left(O_2\right)\)
=> AM là tiếp tuyến chung của \(\left(O_1\right);\left(O_2\right)\)
+) Ta có: \(\hept{\begin{cases}\widehat{BMO_1}=\widehat{AMO_1}\\\widehat{CMO_2}=\widehat{AMO_2}\end{cases}}\)
Ta có; \(\widehat{BMO_1}+\widehat{AMO_1}+\widehat{CMO_2}+\widehat{AMO_2}=180^0\)
\(\Leftrightarrow2\left(\widehat{O_1AM}+\widehat{AMO_2}\right)=180^0\)
\(\Leftrightarrow\widehat{O_1AM}+\widehat{AMO_2}=90^0\)
\(\Leftrightarrow\widehat{O_1MO_2}=90^0\)
\(\Rightarrow O_1M\perp O_2M\)
d) Ta có: \(\widehat{O_1BA}=\widehat{O_1AB}=\widehat{O_2AD}=\widehat{O_2DA}\)
\(\widehat{\Rightarrow O_1BA}=\widehat{O_2DA}\)mà 2 góc này ở vị trí so le trong
\(\Rightarrow O_1B//O_2D\)
\(\Rightarrow\frac{AB}{AD}=\frac{AO_1}{AO_2}\left(1\right)\)
CMTT \(\Rightarrow\frac{AE}{AC}=\frac{AO_1}{AO_2}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\frac{AB}{AD}=\frac{AE}{AC}\)
\(\Rightarrow AB.AC=AD.AE\)
\(\Rightarrow\frac{1}{2}AB.AC=\frac{1}{2}AD.AE\)
\(\Rightarrow S_{\Delta ADE}=S_{\Delta ABC}\)

Ban co de hsg Hai Phong nam 2019-2020 ko cho mik xin voi
a) dung phuong h
b) Ap dung cau a va bien doi mot chut
c) chua nghi ra

Giả thiết:
- - Hai đường tròn (O; R) và (O'; R) cắt nhau tại A và B.
- - Vẽ các bán kính OC và O'D sao cho OC // O'D.
- - Các điểm C và D nằm cùng phía với A so với OO'.
1. Chứng minh AK // BD
- Vì OC // O'D nên ∠COB = ∠DO'B (hai góc so le trong bằng nhau).
- Mà CO và DO' là bán kính, nên tam giác COB và DO'B là hai tam giác có góc tại B bằng nhau và có cạnh OB chung.
- Xét tam giác COB và tam giác DO'B, ta có:
- ∠COB = ∠DO'B
- OB chung
→ ∠CBO = ∠DBO
- Xét tứ giác ABCD:
- A, B là giao điểm của hai đường tròn
- OC và O'D là bán kính nên CO = R = O'D
- OC // O'D ⇒ tam giác COB và DO'B đồng dạng
- Do đó: ∠CAB = ∠DBA (vì cùng bằng ∠COB)
→ ΔAKB và ΔDAB có góc tại K và D bằng nhau,
→ Mà AB là cạnh chung, nên AK // BD (góc so le trong hoặc đồng vị).
Kết luận: AK song song với BD.
2. Chứng minh A là trực tâm tam giác BCD
Ta cần chứng minh rằng A là giao điểm ba đường cao của tam giác BCD.
Ta chứng minh A nằm trên ba đường cao của tam giác BCD, tức là:
- - A là trực tâm của tam giác BCD nếu:
- -- A nằm trên đường vuông góc với CD kẻ từ B,
- -- A nằm trên đường vuông góc với BC kẻ từ D,
- -- A nằm trên đường vuông góc với BD kẻ từ C.
Cách chứng minh:
- - Vì C nằm trên đường tròn (O), D nằm trên đường tròn (O') và OC // O'D ⇒ tứ giác CODD là hình bình hành suy biến hoặc có tính chất đặc biệt.
- - Ta có OC ⊥ AB (vì tam giác COA cân tại O, góc ở A là 90 độ).
- - Tương tự, O'D ⊥ AB ⇒ AB ⊥ CD
→ Suy ra AB ⊥ CD
Tức là: A nằm trên đường vuông góc với CD kẻ từ B
- - Tương tự, ta có thể chứng minh AB ⊥ BC và AB ⊥ BD ⇒ A nằm trên hai đường cao còn lại.
Vậy A là giao điểm ba đường cao của tam giác BCD.
Kết luận: A là trực tâm tam giác BCD.🤡
Em xin tick ạ ! 🥺🥺🤡🤡🤡
Qua A, kẻ tiếp tuyến Ax với (O1) và (O2), Ax cắt BC tại K
Xét (O1) có
KB,KA là các tiếp tuyến
Do đó: KB=KA
Xét (O2) có
KA,KC là các tiếp tuyến
Do đó: KA=KC
mà KA=KB
nên KB=KC
=>K là trung điểm của BC
Xét ΔABC có
AK là đường trung tuyến
\(AK=\frac{BC}{2}\)
Do đó: ΔABC vuông tại A
=>\(\hat{BAC}=90^0\)

a) Theo tính chất hai tiếp tuyến cắt nhau ta có IA = IB = IC.
Do đó tam giác ABC vuông tại A.
Lại có \(IO_1\perp AB;IO_2\perp AC\) nên tam giác \(IO_1O_2\) vuông tại I.
b) Đầu tiên ta chứng minh kết quả sau: Cho hai đường tròn (D; R), (E; r) tiếp xúc với nhau tại A. Tiếp tuyến chung BC (B thuộc (D), C thuộc (E)). Khi đó \(BC=2\sqrt{Rr}\).
Thật vậy, kẻ EH vuông góc với BD tại H. Ta có \(DH=\left|R-r\right|;DE=R+r\) nên \(BC=EH=\sqrt{DE^2-DH^2}=2\sqrt{Rr}\).
Trở lại bài toán: Giả sử (O; R) tiếp xúc với BC tại M.
Theo kết quả trên ta có \(BM=2\sqrt{R_1R};CM=2\sqrt{RR_2};BC=2\sqrt{R_1R_2}\).
Do \(BM+CM=BC\Rightarrow\sqrt{R_1R}+\sqrt{R_2R}=\sqrt{R_1R_2}\Rightarrow\dfrac{1}{\sqrt{R}}=\dfrac{1}{\sqrt{R_1}}+\dfrac{1}{\sqrt{R_2}}\).
P/s: Hình như bạn nhầm đề