Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn có thể cho mih tham khảo hình bạn vẽ dc ko hình mik vẽ hơi fail :)))

x x' y y' O m n
a) +) Vì Ox đối với Ox' và Oy đối với Oy' nên \(\widehat{xOy}\) và \(\widehat{x'Oy'}\) đối đỉnh
\(\Rightarrow\)\(\widehat{xOy}=\)\(\widehat{x'Oy'}\)
hay \(\widehat{x'Oy'}\)\(=40^0\)
+) Ta có: \(\widehat{xOy}+\widehat{x'Oy}=180^0\) (kề bù)
hay \(40^0+\widehat{x'Oy}=180^0\)
\(\Leftrightarrow\widehat{x'Oy}=180^0-40^0\)
\(\Leftrightarrow\widehat{x'Oy}=140^0\)
+) Ta có: \(\widehat{xOy}+\widehat{xOy'}=180^0\) (kề bù)
hay \(40^0+\widehat{xOy'}=180^0\)
\(\Leftrightarrow\widehat{xOy'}=180^0-40^0\)
\(\Leftrightarrow\widehat{xOy'}=140^0\)
b) Vì \(\widehat{xOy}=\widehat{x'Oy'}\)(hai góc đối đỉnh)
Mà Om là tia phân giác của góc xOy và On là tia phân giác của x'Oy' nên Om đối On (đpcm)
y m x O x' n y'
a, Vì góc x'Oy' và góc xOy là hai góc đối đỉnh, mà \(\widehat{xOy}=40^0\)nên \(\widehat{x'Oy'}=40^0\). Góc xOy và góc xOy' là hai góc kề bù nên \(\widehat{xOy}+\widehat{xOy'}=180^0\)hay \(40^0+\widehat{xOy'}=180^0\)
=> \(\widehat{xOy'}=180^0-40^0=140^0\)
Góc xOy' là góc đối đỉnh với góc xOy' nên \(\widehat{xOy}=\widehat{x'Oy}=140^0\)
b, Om,On theo thứ tự là các tia phân giác của hai góc xOy và x'Oy' nên \(\widehat{xOm}=\widehat{mOy}=\frac{1}{2}\widehat{xOy}\)và \(\widehat{nOx'}=\widehat{mOy'}=\frac{1}{2}\widehat{x'Oy'}\)mà \(\widehat{xOy}=\widehat{x'Oy'}\), do đó \(\widehat{xOm}=\widehat{mOy}=\widehat{nOx'}=\widehat{nOy'}=\frac{1}{2}\widehat{xOy}\).
Ta có : \(\widehat{xOm}=\widehat{nOy'}=\widehat{y'Ox}=\widehat{xOm}=\widehat{y'Ox}+\widehat{xOm}+\widehat{mOy}\)
\(=\widehat{y'Ox}+\widehat{xOy}=180^0\)
Góc mOn là góc bẹt,vì thế hai tia Om,On là hai tia đối nhau

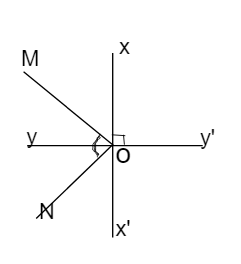
Vì xx' ⊥ yy' tại O (gt)
⇒ ∠x'Oy = 900 (định nghĩa 2 đường thẳng vuông góc)
Ta có: ∠xOy + ∠x'Oy = 1800 (2 góc kề bù)
Thay số: ∠xOy + 900 = 1800
∠xOy = 1800 - 900
∠xOy = 900
Mà OM là tia phân giác của ∠xOy
ON là tia phân giác của ∠yOx'
⇒ ∠mOy = 450
∠yOn = 450
Ta có: ∠mOy + ∠yOn = ∠mOn (2 góc kề nhau)
Thay số: 45+45 = ∠mOn
900 = ∠mOn
∠mOn = 900
Vậy ∠mOn = 900
a) Vì Ot là tia phân giác của x O y ^ nên x O t ^ = t O y ^ = 1 2 x O y ^ (1)
Vì Ot là tia phân giác của y O z ^ nên y O t ' ^ = t ' O z ^ = 1 2 y O z ^ (2)
Từ (1) và (2) ta có: t O t ' ^ = t O y ^ + y O t ' ^ t O t ' ^ = 1 2 x O y ^ + 1 2 y O z ^ = 1 2 x O z ^ (vì x O y ^ và y O z ^ kề bù)
t O t ' ^ = 1 2 .180 0 = 90 0
Vậy t O t ' ^ = 90 0 hay O t ⊥ O t ' .
b) Theo phần a ta có t O t ' ^ = 90 0
Vì Om là tia đối của tia Ot nên m O t ^ = 180 0 và hai góc m O t ^ , t O t ' ^ là hai góc kề bù nên
t O t ' ^ + t ' O m ^ = 180 0 hay 90 0 + t ' O m ^ = 180 0
Suy ra t ' O m ^ = 90 0