Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác vuông AOM và tam giác vuông BƠM có:
Cạnh huyền AM chung
\(\widehat{AOM}=\widehat{BOM}\) (gt)
\(\Rightarrow\Delta AOM=\Delta BOM\) (Cạnh huyền - góc nhọn)
\(\Rightarrow MA=MB;OA=AB\)hay tam giác OAB cân tại O.
b) Xét tam giác vuông AMD và tam giác vuông BME có:
AM = BM
\(\widehat{AMD}=\widehat{BME}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta AMD=\Delta BME\) (Cạnh góc vuông - góc nhọn kề)
\(\Rightarrow MD=ME\)
c) Ta thấy OA = OB; AD = BE nên OD = OE
Vậy thì \(\Delta ODI=\Delta OEI\left(c-g-c\right)\)
\(\Rightarrow\widehat{OID}=\widehat{OIE}\)
Chúng lại là hai góc kề bù nên \(\widehat{OID}=\widehat{OIE}=90^o\) hay MO vuông góc DE.

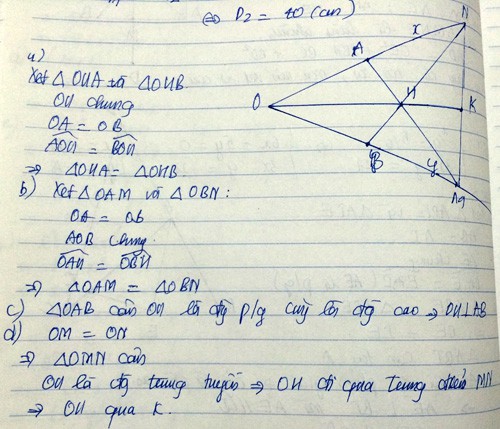
a) Xét Tàm giác vuông OBK và Tam giác vuông OAH có :
OA = OB (GT)
<O chung
=> Tam giác vuông OBK = Tam giác vuông OAH ( cạnh góc vuông - góc nhọn kề )
=> OH = OK (2CTU)
Xét Tam giác OHK có :
OH = OK
=> Tam giác OHK cân tại O (dpcm)
b) Vì Tam giác OBK và Tam giác OAH (cmt)
=> <OKB = <OHA (2GTU)
TC : OH = OK (cmt)
OA = OB (GT)
mà OH = OB + BH
OK = OA + AK
=> AK = BH
Xét Tam giác vuông AIK và Tam giác vuông BIH
AK = BH
<OKB = <OHA
=> Tam giác vuông AIK = Tam giác vuông BIH ( cạnh góc vuông - góc nhọn kề)
=> AI = BI (2CTU)
Xét Tam giác OAI = Tam giác OBI có :
OA = OB (GT)
OI chung
AI = BI (cmt)
=> Tam giác OAI = Tam giác OBI (c.c.c)
=> <AOI = <BOI (2GTU)
=> OI là tia phân giác của <xOy (dpcm)

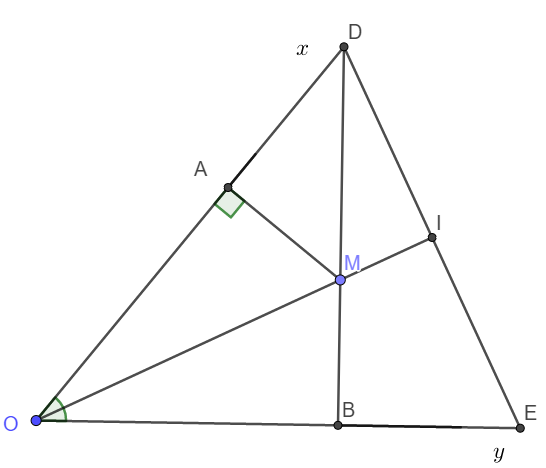
a) Xét ΔOAN vuông tại A và ΔOBN vuông tại B có
ON chung
\(\widehat{AON}=\widehat{BON}\)(ON là tia phân giác của \(\widehat{AOB}\))
Do đó: ΔOAN=ΔOBN(cạnh huyền-góc nhọn)
Suy ra: NA=NB(hai cạnh tương ứng)
b) Ta có: ΔOAN=ΔOBN(cmt)
nên OA=OB(hai cạnh tương ứng)
Xét ΔOAB có OA=OB(cmt)
nên ΔOAB cân tại O(Định nghĩa tam giác cân)
c) Xét ΔAND vuông tại A và ΔBNE vuông tại B có
NA=NB(cmt)
\(\widehat{AND}=\widehat{BNE}\)(hai góc đối đỉnh)
Do đó: ΔAND=ΔBNE(cạnh góc vuông-góc nhọn kề)
Suy ra: ND=NE(hai cạnh tương ứng)
d) Ta có: ΔAND=ΔBNE(cmt)
nên AD=BE(Hai cạnh tương ứng)
Ta có: OA+AD=OD(A nằm giữa O và D)
OB+BE=OE(B nằm giữa O và E)
mà OA=OB(cmt)
và AD=BE(cmt)
nên OD=OE
Ta có: OD=OE(cmt)
nên O nằm trên đường trung trực của DE(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: ND=NE(cmt)
nên N nằm trên đường trung trực của DE(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra ON là đường trung trực của DE
hay ON⊥DE(đpcm)

a: Xét ΔOAN vuông tại A và ΔOBN vuông tại B có
ON chung
\(\widehat{AON}=\widehat{BON}\)
Do đó: ΔOAN=ΔOBN
Suy ra: NA=NB
b: Ta có: ΔOAN=ΔOBN
nên OA=OB
hay ΔOAB cân tại O
c: Xét ΔNAD vuông tại A và ΔNBE vuông tại B có
NA=NB
\(\widehat{AND}=\widehat{BNE}\)
Do đó: ΔNAD=ΔNBE
Suy ra: ND=NE