Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

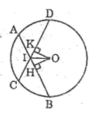
Xét hai tam giác OIH và OIK, ta có :
OI chung
OH = OK (chứng minh trên)
Suy ra: ∆ OIH = ∆ OIK (cạnh huyền, cạnh góc vuông)
Suy ra: IH = IK (1)
Lại có: HA = HB = (1/2).AB
KC = KD = (1/2).CD
Mà AB = CD nên HA = KC (2)
Từ (1) và (2) suy ra: IA = IC
Mà AB = CD nên IB = ID

a: \(\hat{DPB}=\hat{DQB}=90^0\)
=>P,D,Q,B cùng thuộc đường tròn đường kính DB
b: PDQB là tứ giác nội tiếp
=>\(\hat{PQB}=\hat{PDB}=\hat{CDB}\)
Xét (O) có \(\hat{CDB};\hat{CAB}\) là các góc nội tiếp chắn cung CB
=>\(\hat{CDB}=\hat{CAB}=\hat{PAC}\)
=>\(\hat{PAC}=\hat{PQB}\)
c:
Gọi H là giao điểm của PQ và AC
Ta có: \(\hat{PAC}=\hat{PQB}\)
\(\hat{PQB}+\hat{BPQ}=90^0\) (ΔPBQ vuông tại B)
Do đó: \(\hat{PAC}+\hat{BPQ}=90^0\)
mà \(\hat{BPQ}=\hat{APH}\) (hai góc đối đỉnh)
nên \(\hat{PAC}+\hat{APH}=90^0\)
=>PQ⊥AC tại H

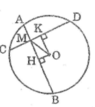
Ta có: HA = HB (gt)
Suy ra : OH ⊥ AB (đường kính dây cung)
Lại có : KC = KD (gt)
Suy ra : OK ⊥ CD (đường kính dây cung)
Mà AB > CD (gt)
Nên OK > OH (dây lớn hơn gần tâm hơn)
Áp dụng định lí Pitago vào tam giác vuông OHM ta có :
O M 2 = O H 2 + H M 2
Suy ra : H M 2 = O M 2 - O H 2 (1)
Áp dụng định lí Pitago vào tam giác vuông OKM ta có:
O M 2 = O K 2 + K M 2
Suy ra: K M 2 = O M 2 - O K 2 (2)
Mà OH < OK (cmt) (3)
Từ (1), (2) và (3) suy ra: H M 2 > K M 2 hay HM > KM



Kẻ OH ⊥ AB, OK ⊥ CD
Ta có: AB = CD (gt)
Suy ra : OH = OK (hai dây bằng nhau cách đều tâm)
Vậy OI là tia phân giác của góc BID (tính chất đường phân giác)