Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra OA là đường trung trực của BC
=>OA⊥BC tại H và H là trung điểm của BC
b: Xét (O) có
ΔBCD nội tiếp
BD là đường kính
Do đó: ΔBCD vuông tại C
=>CB⊥CD
mà OA⊥BC
nên OA//CD
c: Ta có: \(\hat{FBA}+\hat{OBF}=\hat{OBA}=90^0\)
\(\hat{HBF}+\hat{OFB}=90^0\) (ΔBHF vuông tại H)
mà \(\hat{OBF}=\hat{OFB}\) (ΔOBF cân tại O)
nên \(\hat{FBA}=\hat{HBF}\)
=>BF là phân giác của góc HBA
Xét (O) có
ΔBFE nội tiếp
FE là đường kính
Do đó: ΔBFE vuông tại B
=>BF⊥BE
=>BE là phân giác ngoài tại đỉnh B của ΔHBA
Xét ΔHBA có BF là phân giác của góc HBA
nên \(\frac{FH}{FA}=\frac{BH}{BA}\left(3\right)\)
Xét ΔHBA có BE là phân giác ngoài tại đỉnh B
nên \(\frac{EH}{EA}=\frac{BH}{BA}\left(4\right)\)
Từ (3),(4) suy ra \(\frac{FH}{FA}=\frac{EH}{EA}\)
=>\(FH\cdot EA=FA\cdot EH\)
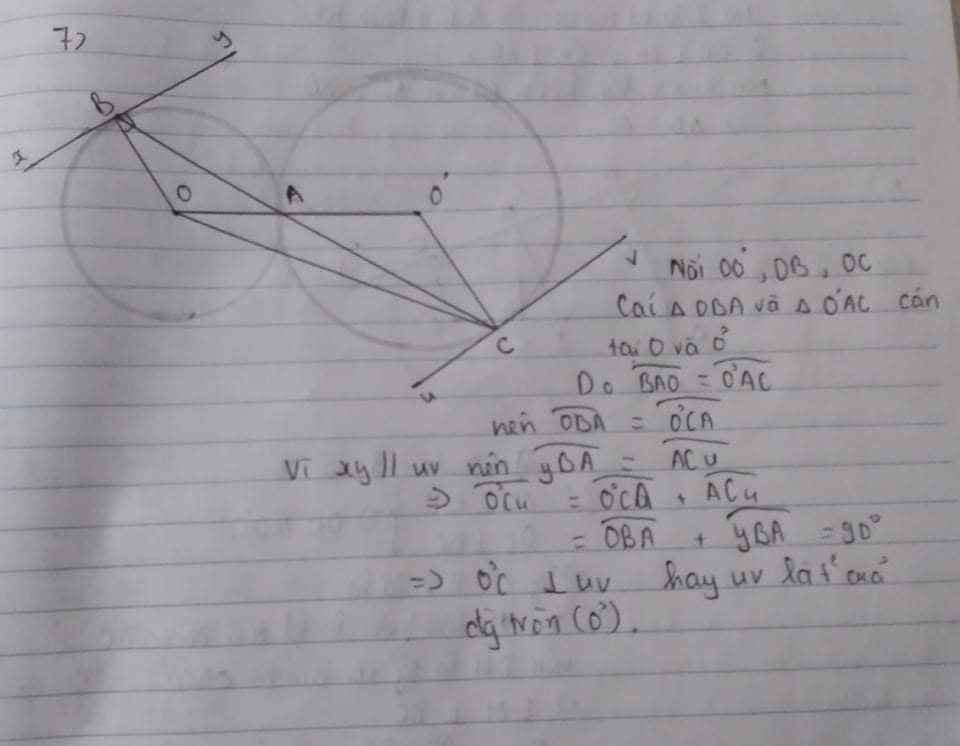
ta có :
\(\widehat{OAB}+\widehat{O'AC}=90^o\Rightarrow\hept{\begin{cases}AC=2AO\cos\widehat{OAC}\\AB=2AO'\cos\widehat{O'AB}=2AO'\sin\widehat{OAC}\end{cases}}\)
ta có : \(S_{ABC}=\frac{1}{2}AB.AC=2OA.O'A.\sin\widehat{OAC}.cos\widehat{OAC}\le OA.O'A\left(\sin^2\widehat{OAC}+cos^2\widehat{OAC}\right)=OA.OA'\)
dấu bằng xảy ra khi \(\sin\widehat{OAC}=cos\widehat{OAC}\Rightarrow\widehat{OAC}=45^o\)
từ đó ta xác định được vị trí của B và C
Chọn đáp án D
Vì hai đường tròn có một điểm chung là A và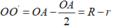
nên hai đường tròn tiếp xúc trong