Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Phân tích bài toán
Giả sử PQ và PR là hai đường xiên kẻ từ P đến d sao cho PQ = PR và\(\widehat{QPR}=60^0\). Gọi H là chân đường vuông góc kẻ từ P đến d. Khi đó ∆PHQ = ∆PHR (cạnh huyền, cạnh góc vuông), suy ra \(\widehat{HPQ}=\widehat{HPR}=30^0\) Từ đó suy ra cách vẽ hai đường xiên PQ và PR.
Kẻ\(PH\perp d\) (H ∈ d). Dùng thước đo góc để vẽ góc HPx bằng 30°. Tia Px cắt d tại điểm Q. Trên d lấy điểm R sao cho HR = HQ. Hai đường xiên PQ và PR lần lượt có hình chiếu trên d là HQ và HR. Do HQ = HR nên PQ = PR.
Hơn nữa\(\widehat{QPR}=2\widehat{HQP}=60^0\)
b) Hướng dẫn
- Tam giác PQR có PQ = PR và \(\widehat{QPR}=60^0\), tam giác PQR là tam giác đều
PQ = 18cm => QR =18cm ; HQ = HR =9cm.
Giả sử PQ và PR là hai đường xiên kẻ từ P đến d sao cho PQ = PR và ∠(QPR) = 60°.
Gọi H là chân đường vuông góc kẻ từ P đến d. Khi đó ΔPHQ = ΔPHQ (cạnh huyền, cạnh góc vuông),
suy ra ∠(HPQ) = ∠(HPR) = 30°. Từ đó suy ra cách vẽ hai đường xiên PQ và PR.
Kẻ PH ⊥ d (H ∈ d).
Dùng thước đo góc để vẽ góc HPx bằng 30°.
Tia Px cắt d tại điểm Q. Trên d lấy điểm R sao cho HR = HQ.
Hai đường xiên PQ và PR lần lượt có hình chiếu trên d là HQ và HR.
Do HQ = HR nên PQ = PR.
Hơn nữa ∠(QPR) = 2∠(HPQ) = 60°.
b) Hướng dẫn
- Tam giác PQR có PQ = PR và ∠(QPR) = 60°, tam giác đó là tam giác đều
- PQ = 18cm ⇒ QR =18 cm ; HQ = HR =9 cm

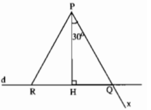
+ Hình chiếu của PQ và PR chính là HQ và HR.
+ ΔPQR có PQ = PR và ∠P = 60o
⇒ ΔPQR đều
⇒ QR = PQ = 18cm.
+ ΔPHQ = ΔPHR ( cạnh huyền- cạnh góc vuông) ⇒ QH = HR = 1/2.QR = 9cm.
Vậy độ dài hình chiếu của PQ và PR trên d đều bằng 9cm.

a: Xét ΔABC có
N,M lần lượt là trung điểm của AB,AC
=>NM là đường trung bình của ΔABC
=>NM//BC và \(NM=\frac{BC}{2}\)
Xét ΔOBC có
P,Q lần lượt là trung điểm của OB,OC
=>PQ là đường trung bình của ΔOBC
=>PQ//BC và \(PQ=\frac{BC}{2}\)
Ta có: NM//BC
PQ//BC
Do đó: MN//PQ
Ta có: \(MN=\frac{BC}{2}\)
\(PQ=\frac{BC}{2}\)
Do đó: MN=PQ
b: Xét ΔMAB và ΔMCE có
\(\hat{MAB}=\hat{MCE}\) (hai góc so le trong, AB//CE)
MA=MC
\(\hat{AMB}=\hat{CME}\) (hai góc đối đỉnh)
Do đó: ΔMAB=ΔMCE
c: Gọi X là giao điểm của AF và BC
Xét ΔABC có
BM,CN là các đường trung tuyến
BM cắt CN tại O
Do đó: O là trọng tâm của ΔABC
=>AO cắt BC tại trung điểm của BC
=>X là trung điểm của BC
Xét ΔABC có
AX là đường trung tuyến
O là trọng tâm
Do đó: AO=2OX
mà AO=OF
nên OF=2OX
=>X là trung điểm của OF
Xét ΔABC có
BM là đường trung tuyến
O là trọng tâm
Do đó: BO=2OM
Xét tứ giác BOCF có
X là trung điểm chung của BC và OF
=>BOCF là hình bình hành
=>CF=BO=2OM


+ Phân tích bài toán
Giả sử PQ và PR là hai đường xiên kẻ từ P đến d sao cho PQ = PR và ∠(QPR) = 60o.
Gọi H là chân đường vuông góc kẻ từ P đến d.
Khi đó ΔPHQ = ΔPHR (cạnh huyền, cạnh góc vuông)
⇒ ∠(HPQ) = ∠(HPR) = 30o.
+ Từ đó suy ra cách vẽ hai đường xiên PQ và PR:
- Kẻ PH ⊥ d (H ∈ d)
- Kẻ các tia Px, Py tạo với PH 1 góc 30o (Py, Px thuộc hai nửa mp bờ là đường thẳng PH)
- Px, Py cắt d lần lượt tại Q và R.
Khi đó ΔPHQ = ΔPHR nên PQ = PR và ∠QPR = 60o.