Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


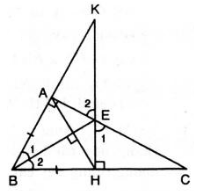
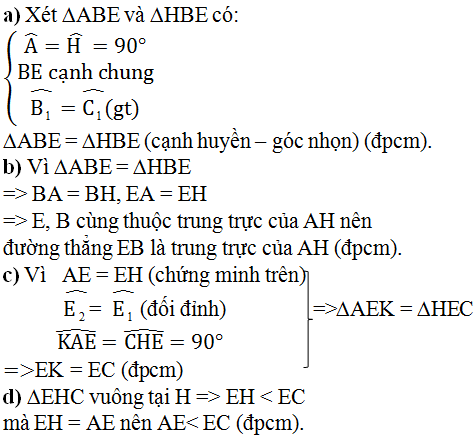
a) Xét hai tam giác vuông tam giác ABE và tam giác HBE ta có:
góc B1 = góc B2 (BE là phân giác của góc B)
BE: cạnh chung
=> tam giác ABE = tam giác HBE (cạnh huyền - góc nhọn)

Câu a
Xét tam giác ABD và AMD có
AB = AM từ gt
Góc BAD = MAD vì AD phân giác BAM
AD chung
=> 2 tam guacs bằng nhau
Câu b
Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD
Bd = bm vì 2 tam giác ở câu a bằng nhau
Góc BDE bằng MDC đối đỉnh
=> 2 tam giác bằng nhau

a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔBAE=ΔBHE
b: ta có: ΔBAE=ΔBHE
nên BA=BH và EA=EH
=>EB là đường trug trực của AH
c: Xét ΔAEK vuông tại A và ΔHEC vuông tại H có
EA=EH
\(\widehat{AEK}=\widehat{HEC}\)
Do đo: ΔAEK=ΔHEC
Suy ra: EK=EC

Trả lời................
Tớ không biết đúng hay sai đâu nha Ý Phạm
a,Xét tam giác ABE (BAE^ vuông) và tam giác HBE (BHE^ vuông) có:
BE=BE (cạnh chung)
ABE^=HBE^
⟹ ABE^=HBE^(ch+gn)
b,Ta có:
BA=BH (tam giác ABE = tam giác HBE)
EA=EH (________________________)
⟹ BE là đường trung trực của AH
c,Xét tam giác EKA và tam giác ECH có
AE=EH (gt)
EAK^=EHK^(=90o)
AEK^=HEC^(đối đỉnh)
⟹Tam giác EKA=tam giacsEHK (g-c-g)
⟹EK=EH ( cạnh tương ứng)
d,Từ điểm E đến đường thẳng HC có:
EH là đường vuông góc
EC là đường xiên
⟹EH<EC( quan hệ đường vuông góc)
Mà EH=AE(tam giác ABE = tam giác HBE)
⟹AE<AC

đề ngay chỗ K là giao điểm của AB và HE là sao mk vẽ ko được???
8789

E A B H C 1 2
Cm: a) Xét t/giác ABE và t/giác HBE
có góc A = góc H1 = 900 (gt)
BE : chung
góc ABE = góc EBH (gt)
=> t/giác ABE = t/giác HBE (ch - gn)
b) Ta có: t/giác ABE = t/giác HBE (cmt)
=> AE = EH (hai cạnh tương ứng) (1)
Xét t/giác EHC có góc H2 = 900
=> EC > EH (cạnh đối diện với góc vuông là cạnh lớn nhất) (2)
Từ (1) và (2) suy ra EA < EC (Đpcm)



xét \(\Delta abe\)và \(\Delta hbe\)có:
\(\widehat{BAE}=\widehat{BHE}=90^O\)
BE LÀ CẠNH CHUNG
\(\widehat{ABE}=\widehat{HBE}\)(vì BE là đường phân giác của \(\widehat{B}\))
DO ĐÓ : T/G ABE = T/G HBE (G-C-G)
b, tam giác ABE = tam giác HBE (Câu a)
=> EA = EH (đn)
tam giác EHC vuông tại H do EH _|_ BC (gt) => EH < EC
=> AE < EC (tcbc)