Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C H N M 3 4
Xét \(\Delta HAC\)vuông tại H có HN là đường trung tuyến ứng với cạnh huyền
=> HN = NC = NA = AC/2
=> AC = 2HN = 8
Tương tự AB = 6
Theo hệ thức lượng trong tam giác vuông cho tam giác ABC vuông tại A có AH là đường cao thì
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{1}{6^2}+\frac{1}{8^2}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{25}{576}\)
\(\Leftrightarrow AH=\frac{24}{5}\)
Áp dụng định lí Pytago vào \(\Delta HAC\)vuông tại H có
\(HA^2+HC^2=AC^2\)
\(\Leftrightarrow\left(\frac{24}{5}\right)^2+HC^2=8^2\)
\(\Leftrightarrow HC=\frac{32}{5}\)
Tương tự \(HB=\frac{18}{5}\)

a) Ta có tứ giác MHNA là hình chữ nhật
\(\Rightarrow\widehat{AMN}=\widehat{AHN}\) ( góc nội tiếp cùng chắn cung AN)
mà \(\widehat{AHN}=\widehat{ACH}\) ( cùng phụ với \(\widehat{HAN}\) )
\(\Rightarrow\widehat{AMN}=\widehat{ACH}\)
Xét \(\Delta AMN\) và \(\Delta ACB\) có:
\(\left\{{}\begin{matrix}\widehat{AMN}=\widehat{ACH}\left(cmt\right)\\\widehat{MAN}chung\end{matrix}\right.\)
\(\Rightarrow\Delta AMN\sim\Delta ACB\left(g.g\right)\)
\(\Rightarrow\frac{AM}{AC}=\frac{AN}{AB}\Rightarrow AM.AB=AN.AC\left(đpcm\right)\)
b) Xét \(\Delta AHB\) vuông tại H, \(MH\perp AB\) có:
\(MH^2=MA.MB\left(1\right)\)
cmtt: \(NH^2=NA.NC\left(2\right)\)
Ta lại có: \(HB.HC=AH^2=MN^2\)( 2 đường chéo bằng nhau) (3)
Xét \(\Delta MHN\) vuông tại H có
\(\Rightarrow MH^2+HN^2=MN^2=AH^2\left(4\right)\)
Từ (1),(2),(3) và (4) \(\Rightarrow HB.HC=MA.MB+NA.NC\left(đpcm\right)\)
c) Có \(HB=\frac{AC^2}{BC}\)
\(HC=\frac{AC^2}{BC}\)
\(\Rightarrow\frac{BH}{HC}=\frac{AB^2}{BC}:\frac{AC^2}{BC}=\frac{AB^2}{AC^2}=\left(\frac{AB}{AC}\right)^2\)

A B C H M N
Vì M là trung điểm của AB => HM là trung tuyến
Mà \(\Delta ABH\)vuông tại H
=> \(HM=\frac{1}{2}AB\)( trong tam giác vuông trung tuyến ứng với cạnh huyền = 1 phần 2 cạnh huyền )
=> AB = 30 cm
Chứng minh tương tự
=> AC= 40 cm
Xét \(\Delta ABC\)có ( A = 900 )
=> \(BC=\sqrt{AC^2+AB^2}=50\)cm
Áp dụng hệ thức cạnh trong tam giác vuông ta có :
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
\(\Rightarrow\frac{1}{AH}=\sqrt{\frac{1}{AB^2}+\frac{1}{AC^2}}=\frac{1}{24}\)
\(\Rightarrow AH=24cm\)
Áp dụng hệ thức cạnh trong tam giác vuông ta có :
\(AB^2=BH.BC\)
\(\Rightarrow BH=AB^2:BC=18cm\)
Vì BH + HC = BC
\(\Rightarrow HC=50-18=32cm\)
Study well

a/ Có tứ giác MHNA là hcn\(\Rightarrow\widehat{AMN}=\widehat{AHN}\) (góc nt cùng chắn \(\stackrel\frown{AN}\))
Mà \(\widehat{AHN}=\widehat{ACH}\) (cùng phụ vs \(\widehat{HAN}\))
\(\Rightarrow\widehat{AMN}=\widehat{ACH}\)
Xét \(\Delta AMN\) và \(\Delta ACB\) có:
\(\widehat{AMN}=\widehat{ACH}\left(CMT\right)\)
\(\widehat{MAN}\) : góc chung
\(\Rightarrow\Delta AMN\sim\Delta ACB\left(gg\right)\)
\(\Rightarrow\frac{AM}{AC}=\frac{AN}{AB}\Leftrightarrow AM.AB=AN.AC\)
b/ Có \(HB=\frac{AB^2}{BC}\)
\(HC=\frac{AC^2}{BC}\)
\(\Rightarrow\frac{HB}{HC}=\frac{\frac{AB^2}{BC}}{\frac{AC^2}{BC}}=\frac{AB^2}{AC^2}=\left(\frac{AB}{AC}\right)^2\)
c/ Xét \(\Delta AHB\) vuông tại H,\(MH\perp AB\)
\(\Rightarrow MA.MB=MH^2\)(1)
tương tự\(\Rightarrow NA.NC=HN^2\) (2)
\(HB.HC=AH^2=MN^2\) (2 đường chéo bằng nhau)(3)
Xét \(\Delta MHN\) vuông tại H
\(\Rightarrow MH^2+HN^2=MN^2=AH^2\)(4)
Từ (1),(2),(3),(4)\(\Rightarrow HB.HC=MA.MB+NA.NC\)

a) Áp dụng hệ thức lượng trong \(\Delta vAHB\), ta có:
\(AH^2=AM\cdot AB\left(1\right)\)
Áp dụng hệ thức lượng trong \(\Delta vAHC\), ta có:
\(AH^2=AN\cdot AC\left(2\right)\)
Từ(1) và (2) ta được: \(AM\cdot AB=AN\cdot AC\)
b) Ta có: MHNA là hình chữ nhật(pn tự cm nha cái này dễ)
\(\Rightarrow MH=AN\)
Áp dụng hệ thức lượng trong \(\Delta vAHC\), ta có:
\(HN^2=AN\cdot NC\)
Áp dụng hệ thức lượng trong \(\Delta vAHB\), ta có:
\(HM^2=AM\cdot MB\)
Áp dụng hệ thức lượng trong \(\Delta vAHN\), ta có:
\(AN^2+HN^2=AH^2\)
Mà \(MH=AN\)
\(\Rightarrow MH^2+HN^2=AH^2\)
\(\Rightarrow BM\cdot MA+AN\cdot NC=BH\cdot HC\)
c) Áp dụng hệ thức lượng trong \(\Delta vABC\), ta có:
\(AC^2=HC\cdot BC\left(1\right)\)
Áp dụng hệ thức lượng trong \(\Delta vABC\), ta có:
\(AB^2=HB\cdot BC\left(2\right)\)
Lấy (2) chia (1) ta được: \(\dfrac{HB}{HC}=\left(\dfrac{AB}{AC}\right)^2\)
d) Áp dụng hệ thức lượng trong \(\Delta vABC\), ta có:
\(AC^2=HC\cdot BC\Rightarrow AC^4=HC^2\cdot BC^2\)
\(\Rightarrow AC^4=NC\cdot AC\cdot BC^2\Rightarrow AC^3=NC\cdot BC^2\left(1\right)\)
Áp dụng hệ thức lượng trong \(\Delta vABC\), ta có:
\(AB^2=HB\cdot BC\Rightarrow AB^4=HB^2\cdot BC^2\)
\(\Rightarrow AB^4=BM\cdot AB\cdot BC^2\Rightarrow AB^3=BM\cdot BC^2\left(2\right)\)
Lấy (2) chia (1) ta được: \(\dfrac{BM}{CN}=\left(\dfrac{AB}{AC}\right)^3\)

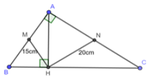
Xét ∆ ABC vuông tại A có M là trung điểm AB
=> HM là đường trung tuyến ứng với cạnh huyền AB
=> HM = 1 2 AB => AB = 2HM = 2. 15 = 30 (cm)
Xét ∆ ACH vuông tại H có N là trung điểm AC
=> HN là đường trung tuyến ứng với cạnh huyền AC
=> HN = 1 2 AC => AC = 2HN = 2. 20 = 40 (cm)
Áp dụng định lý Pitago cho ABH vuông tại A có:
![]()
![]()
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
![]()
Ta có: HC = BC – BH = 50 – 18 = 32 (cm)
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
AH.BC = AB.AC => AH.50 = 30.40 => AH = 24 (cm)
Đáp án cần chọn là: D
B M A N C H
Tam giác AHB vuông tại H có HM là trung tuyến
=> HM = 1/2 AB => AB = 30 cm
Tam giác AHC vuông tại H có HN là trung tuyến
=> HN = 1/2 AC => AC = 40 cm
Áp dụng Pytago ta có: AB2 + AC2 = BC2
=> BC2 = 302 + 402 = 2500
=> BC = 50
Áp dụng hệ thức lượng ta có:
AB2 = BH.BC => \(BH=\frac{AB^2}{BC}=18\)
AC2 = CH.BC => \(CH=\frac{AC^2}{BC}=32\)
HA.BC = AB.AC => \(HA=\frac{AB.AC}{BC}=24\)