Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

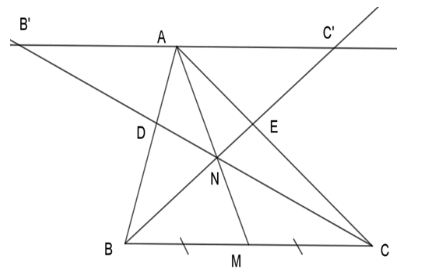
Kẻ đường thẳng đi qua AA song song với BCBC lần lượt cắt CDCD và BEBE kéo dài tại B′B′ và C′C′.
Vì M là trung điểm của BCBC nên BM=MCBM=MC.
Vì AB′//MCAB′//MC, áp dụng định lý Talet ta có:
ANNM=AB′MCANNM=AB′MC (1)
Vì AC′//BMAC′//BM, áp dụng định lý Talet ta có:
ANNM=AC′BMANNM=AC′BM (2)
Từ (1) và (2) ta có: AB′MC=AC′BMAB′MC=AC′BM
Ta có MM là trung điểm của BCBC ⇒⇒BM=MCBM=MC⇒⇒AB′=AC′AB′=AC′ (*)
Vì AB′//BCAB′//BC, áp dụng định lý Talet ta có:
ADDB=AB′BCADDB=AB′BC (**)
Vì AC′//BCAC′//BC, áp dụng định lý Talet ta có:
AEEC=AC′BCAEEC=AC′BC (***)
Từ (*), (**) và (***) ta có:
ADDB=AB′BC=AEEC=AC′BCADDB=AB′BC=AEEC=AC′BC
⇒ADDB=AEEC⇒ADDB=AEEC⇔ADBD=AECE⇔ADBD=AECE hay DE//BC
#vunggoi#

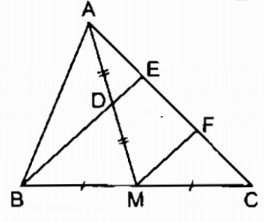
Gọi F là trung điểm của EC
Trong ∆ CBE ta có:
M là trung điểm của cạnh CB
F là trung điểm của cạnh CE
Nên MF là đường trung bình của ∆ CBE
⇒ MF // BE (tính chất đường trung bình của tam giác)
Hay DE // MF
Trong tam giác AMF ta có:
D là trung điểm của AM
DE // MF
Suy ra: AE = EF (tính chất đường trung bình của tam giác)
Mà EF=FC=\(\dfrac{EC}{2}\) nên AE=\(\dfrac{EC}{2}\)

Từ M kẻ MK//DE ,MKcắt AC tại K
Xét tg AMK có:
DE//MK
D là tr.điểm AM
=>E là tr.điểm AK
=>AE=EK=1/2AK
Xét tg BEC có:
BE//MK (do DE//MK)
M là tr.điểm BC (AM là tr.tuyến của tg ABC)
=>K là tr.điểm EC
=>KE=1/2EC
Mà AE=EK (cmt)
=>AE=1/2EC (đpcm)

Xét ΔBEC có
M là trung điểm của BC
F là trung điểm của EC
Do đó: MF là đường trung bình của ΔBEC
Suy ra: MF//DE
Xét ΔAMF có
D là trung điểm của AM
DE//MF
Do đó: E là trung điểm của AF
Suy ra: AE=EF
mà EF=FC
nên AE=FE=FC
hay \(AE=\dfrac{EC}{2}\)


bạn ơi điểm E ở đâu thế???