Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. hạ đương cao AK
suy ra BK=KC=3:2=1.5(cm)
Xét tam giac ABC có góc AKB=90
AK^2+BK^2=AB^2(đl py-ta-go)
AK=\(\dfrac{3\sqrt{3}}{2}\)
SABC=\(\dfrac{1}{2}.\dfrac{3\sqrt{3}}{2}.3=\dfrac{9\sqrt{3}}{4}\)

\(a^2+b^2+c^2+d^2+e^2\ge a\left(b+c+d+e\right)\)
\(\Leftrightarrow4a^2+4b^2+4c^2+4d^2+4e^2\ge4ab+4ac+4ad+4ae\)
\(\Leftrightarrow4a^2+4b^2+4c^2+4d^2+4e^2-4ab-4ac-4ad-4ae\ge0\)
\(\Leftrightarrow\left(a^2-4ab+4b^2\right)+\left(a^2-4ac+4c^2\right)+\left(a^2-4ad+4d^2\right)+\left(a^2-4ae+4e^2\right)\ge0\)
\(\Leftrightarrow\left(a-2b\right)^2+\left(a-2c\right)^2+\left(a-2d\right)^2+\left(a-2e\right)^2\ge0\)( luôn đúng )
Vậy ...

Không mất tính tổng quát,
Giả sử a<b
Ta có: ab=bc => c<b
Ta có: bc=cd => c<d
Ta có: cd=de => e<d
Ta có: de=ea => a>e
Ta có: ea=ab => a>b ( trái với giả sử)
Vậy a=b=c=d=e
=> ba=bc=cd=de=ea
e<a

\(\Leftrightarrow4a^2+4b^2+4c^2+4d^2+4e^2\ge4ab+4ac+4ad+4ae\)
<=>(a2-4ab+4b2)+(a2-4ac+4c2)+(a2-4ad+4d2)+(a2-4ae+e2)\(\ge\)0
<=>(a-2b)2+(a-2c)2+(a-2d)2+(a-2e)2\(\ge\)0 (luôn đúng)
=>dpcm

Xét hiệu:
\(a^2+b^2+c^2+d^2+e^2-a\left(b+c+d+e\right)\)
\(=a^2+b^2+c^2+d^2+e^2-ab-ac-ad-ae\)
\(=\left(\frac{a^2}{4}-ab+b^2\right)+\left(\frac{a^2}{4}-ac+c^2\right)+\left(\frac{a^2}{4}-ad+d^2\right)+\left(\frac{a^2}{4}-ae+e^2\right)\)
\(=\left(\frac{a}{2}-b\right)^2+\left(\frac{a}{2}-c\right)^2+\left(\frac{a}{2}-d\right)^2+\left(\frac{a}{2}-e\right)^2\)
Do \(\left(\frac{a}{2}-b\right)^2\ge0\forall a,b;\left(\frac{a}{2}-c\right)^2\ge0\forall a,c\);\(\left(\frac{a}{2}-d\right)^2\ge0\forall a,d;\left(\frac{a}{2}-e\right)^2\ge0\forall a,e\)Do đó:
\(\left(\frac{a}{2}-b\right)^2+\left(\frac{a}{2}-c\right)^2+\left(\frac{a}{2}-d\right)^2+\left(\frac{a}{2}-e\right)^2\ge0\)
\(\Rightarrow a^2+b^2+c^2+d^2+e^2-a\left(b+c+d+e\right)\ge0\)
\(\Leftrightarrow a^2+b^2+c^2+d^2+e^2\ge a\left(b+c+d+e\right)\)
Dấu"="xảy ra khi \(b=c=d=e=\frac{a}{2}\)
ô kê :))
a2 + b2 + c2 + d2 + e2 ≥ a( b + c + d + e )
<=> a2 + b2 + c2 + d2 + e2 ≥ ab + ac + ad + ae
Nhân 4 vào từng vế ta được
<=> 4( a2 + b2 + c2 + d2 + e2 ) ≥ 4( ab + ac + ad + ae )
<=> 4a2 + 4b2 + 4c2 + 4d2 + 4e2 ≥ 4ab + 4ac + 4ad + 4ae
<=> 4a2 + 4b2 + 4c2 + 4d2 + 4e2 - 4ab - 4ac - 4ad - 4ae ≥ 0
<=> ( a2 - 4ab + 4b2 ) + ( a2 - 4ac + 4c2 ) + ( a2 - 4ad + 4d2 ) + ( a2 - 4ae + 4e2 ) ≥ 0
<=> ( a - 2b )2 + ( a - 2c )2 + ( a - 2d )2 + ( a - 2e )2 ≥ 0 ( đúng )
Vậy bđt được chứng minh
Dấu "=" xảy ra <=> b = c = d = e = a/2

\(a^2+b^2+c^2+d^2+e^2\ge a\left(b+c+d+e\right)\)
\(\Leftrightarrow4a^2+4b^2+4c^2+4d^2+4e^2-4ab-4ac-4ad-4ae\ge0\)
\(\Leftrightarrow\left(a^2-4ab+4b^2\right)+\left(a^2-4ac+4c^2\right)+\left(a^2-4ad+4d^2\right)+\left(a^2-4ae-4e^2\right)\ge0\)
\(\Leftrightarrow\left(a-2b\right)^2+\left(a-2c\right)^2+\left(a-2d\right)^2+\left(a-2e\right)^2\ge0\)
BĐT trên đúng, mà các phép biến đổi là tương đương
\(\RightarrowĐPCM\)
Dấu "=" xảy ra khi a = 2b = 2c = 2d = 2e
Bất đẳng thức đã cho tương đương với:
\[{a^2} + {b^2} + {c^2} + {d^2} + {e^2} - a\left( {b + c + d + e} \right) \ge 0\]
\[ \Leftrightarrow {a^2} - a\left( {b + c + d + e} \right) + {b^2} + {c^2} + {d^2} + {e^2} \ge 0\]
Xét tam thức bậc hai: $f\left( a \right) = {a^2} - a\left( {b + c + d + e} \right) + {b^2} + {c^2} + {d^2} + {e^2}$
Ta có: $\Delta = {\left( {b + c + d + e} \right)^2} - 4\left( {{b^2} + {c^2} + {d^2} + {e^2}} \right)$
Theo bất đẳng thức BCS, ta có: \[{\left( {b + c + d + e} \right)^2} \le \left( {1 + 1 + 1 + 1} \right)\left( {{b^2} + {c^2} + {d^2} + {e^2}} \right) = 4\left( {{b^2} + {c^2} + {d^2} + {e^2}} \right)\]
Suy ra: \[\Delta = {\left( {b + c + d + e} \right)^2} - 4\left( {{b^2} + {c^2} + {d^2} + {e^2}} \right) \le 0 \Rightarrow f\left( a \right) \ge 0,\,\,\forall a \in \mathbb{R} \]
Từ đó ta có đpcm.

đăng từng câu 1 thôi, nhiều nhất là 3 câu/ 1 lần hỏi vì đâu có giới hạn số lần hỏi
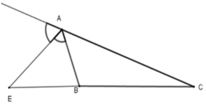
Vì trong tam giác, đường phân giác của một góc chia cạnh đối diện thanh hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy nên A B A C = B E C E
Đáp án D