K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 12 2018
2) \(S=a+\frac{1}{a}=\frac{15a}{16}+\left(\frac{a}{16}+\frac{1}{a}\right)\)
Áp dụng BĐT AM-GM ta có:
\(S\ge\frac{15a}{16}+2.\sqrt{\frac{a}{16}.\frac{1}{a}}=\frac{15.4}{16}+2.\sqrt{\frac{1}{16}}=\frac{15}{4}+2.\frac{1}{4}=\frac{15}{4}+\frac{1}{2}=\frac{15}{4}+\frac{2}{4}=\frac{17}{4}\)
\(S=\frac{17}{4}\Leftrightarrow a=4\)
Vậy \(S_{min}=\frac{17}{4}\Leftrightarrow a=4\)
T
9 tháng 12 2018
kudo shinichi sao cách làm giống của thầy Hồng Trí Quang vậy bạn?
\(S=a+\frac{1}{a}=\frac{15}{16}a+\left(\frac{a}{16}+\frac{1}{a}\right)\ge\frac{15}{16}a+2\sqrt{\frac{1.a}{16.a}}=\frac{15}{16}a+2.\frac{1}{4}\)
\(=\frac{15}{16}.4+\frac{1}{2}=\frac{17}{4}\Leftrightarrow a=4\)
Dấu "=" xảy ra khi a = 4
Vậy \(S_{min}=\frac{17}{4}\Leftrightarrow a=4\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 5 2021
Ngắn gọn thì đây là 1 bài toán không giải được (min max tồn tại, nhưng không thể tìm được)
Cực trị xảy ra tại \(x=\dfrac{a}{b}\) là nghiệm của pt bậc 4:
\(7x^4+11x^3-3x^2-4x-2=0\)
Là một pt không thể phân tích về các pt bậc thấp hơn
25 tháng 2 2023
a: Khi x=16/9 thì \(A=\left(\dfrac{4}{3}-2\right):\left(\dfrac{4}{3}-3\right)=\dfrac{-2}{3}:\dfrac{-5}{3}=\dfrac{2}{5}\)
b: \(=\dfrac{x+2\sqrt{x}+3\sqrt{x}-6-9\sqrt{x}-10}{x-4}\)
\(=\dfrac{x-4\sqrt{x}-16}{x-4}\)
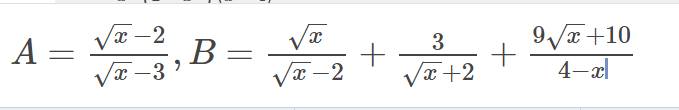
Áp dụng BĐT cosi ta có:
`a^2+1>=2a`
`<=>a^2+2b+3>=2a+2b+2`
Hoàn toàn tương tự:
`b^2+2a+3>=2a+2b+2`
`<=>(a^2+2b+3)(b^2+2a+3)>=(2a+2b+2)^2`
Áp dụng BĐT cosi sau:`xy<=(x+y)^2/4`
`<=>(2a+1)(2b+1)<=(2a+2b+2)^2/4`
`<=>P>=(2a+2b+2)^2/((2a+2b+2)^2/4)`
`<=>P>=4`
Dấu "=" xảy ra khi `a=b=1`