Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
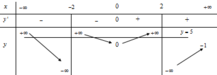
\(\lim\limits_{x\rightarrow\infty}\frac{3x-2}{x+1}=3\Rightarrow y=3\) là tiệm cận ngang
2.
\(\lim\limits_{x\rightarrow2}\frac{-2x}{x-2}=\infty\Rightarrow x=2\) là tiệm cận đứng
3.
\(\lim\limits_{x\rightarrow\infty}\frac{x-2}{x^2-1}=0\Rightarrow y=0\) là tiệm cận ngang
4.
\(\lim\limits_{x\rightarrow\infty}\frac{x-1}{x^2-x}=0\Rightarrow y=0\) là tiệm cận ngang
\(\lim\limits_{x\rightarrow0}\frac{x-1}{x^2-x}=\infty\Rightarrow x=0\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow1}\frac{x-1}{x^2-x}=1\) hữu hạn nên \(x=1\) ko phải tiệm cận đứng
ĐTHS có 2 tiệm cận

Đáp án C
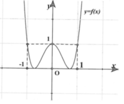
Vì phương trình ![]() có ba nghiệm phân biệt nên đồ thị hàm số
có ba nghiệm phân biệt nên đồ thị hàm số 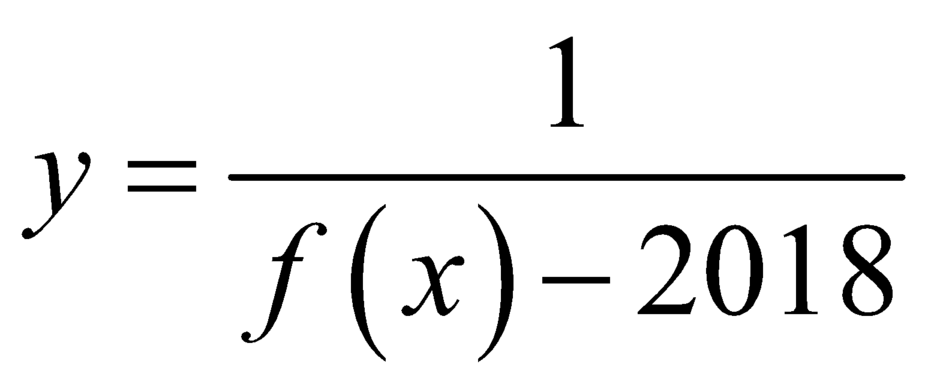 có ba đường tiệm cận đứng.
có ba đường tiệm cận đứng.
Mặt khác, ta có:
![]()
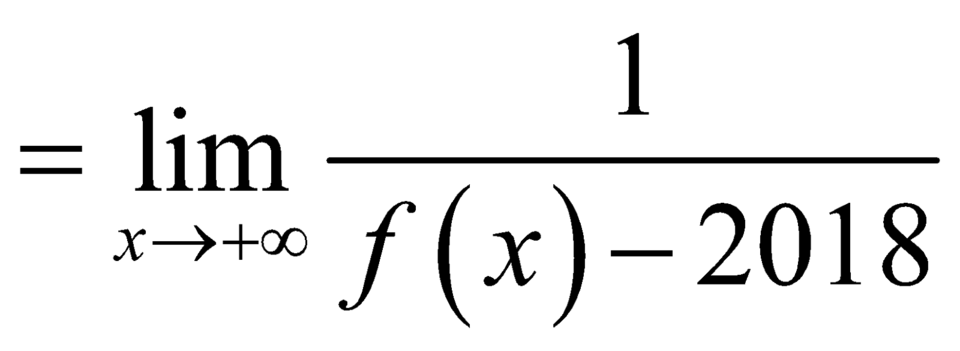
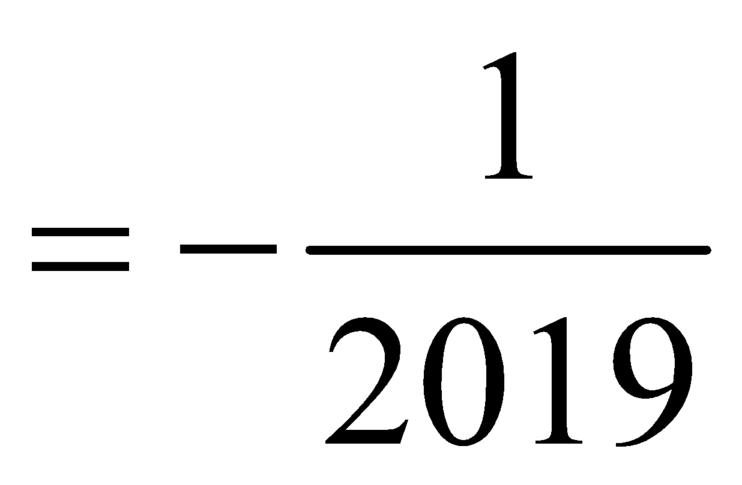 nên đường thẳng
nên đường thẳng ![]() là đường tiệm cận ngang của đồ thị hàm số
là đường tiệm cận ngang của đồ thị hàm số 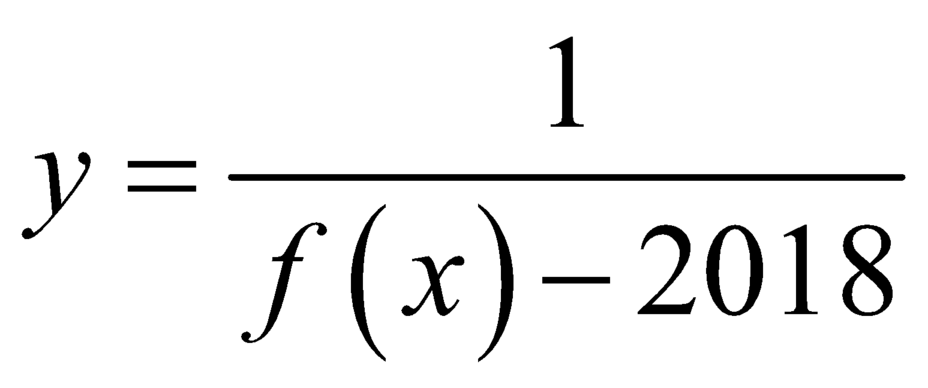 .
.
Và ![]()
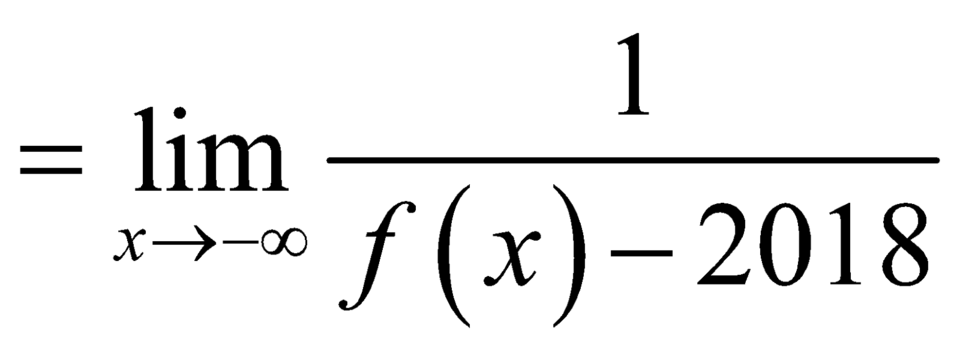
![]() nên đường thẳng y=0 là đường tiệm cận ngang của đồ thị hàm số
nên đường thẳng y=0 là đường tiệm cận ngang của đồ thị hàm số 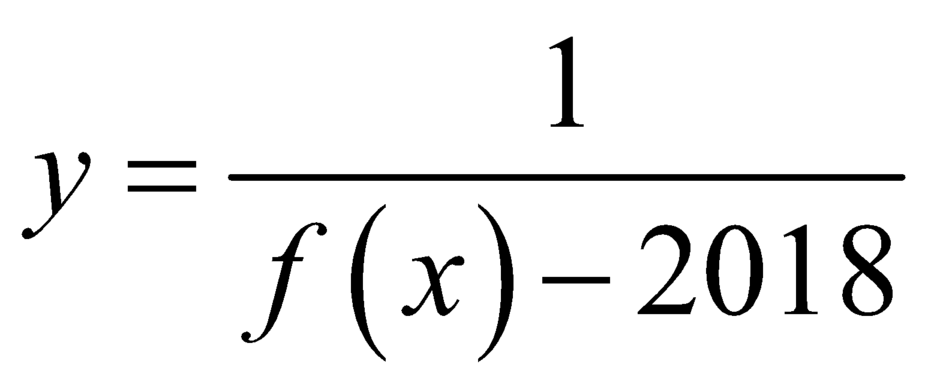 .
.
Vậy ![]() .
.

Chọn A
Đk để hàm số xác định là: ![]() . Vậy mệnh đề
. Vậy mệnh đề ![]() đúng.
đúng.
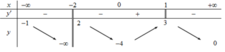
Do hàm số có tập xác định ![]() nên không tồn tại
nên không tồn tại ![]() do đó đồ thị hàm số này không có đường tiệm cận ngang. Vậy mệnh đề
do đó đồ thị hàm số này không có đường tiệm cận ngang. Vậy mệnh đề ![]() sai.
sai.
Do ![]() nên đồ thị hàm số có
nên đồ thị hàm số có ![]() đường tiệm cận đứng là
đường tiệm cận đứng là ![]() và
và ![]() . Vậy
. Vậy ![]() đúng.
đúng.
Ta có
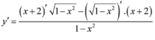
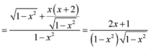
Do ![]() bị đổi dấu qua
bị đổi dấu qua ![]() nên hàm số có một cực trị. Vậy mệnh đề
nên hàm số có một cực trị. Vậy mệnh đề ![]() đúng.
đúng.
Do đó số mệnh đề đúng là ![]() .
.

Đáp án: A.
Nhận xét rằng hàm số dạng 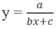 (a, b ≠ 0) có tiệm cận đứng là
(a, b ≠ 0) có tiệm cận đứng là 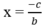 và tiệm cận ngang là y = 0.
và tiệm cận ngang là y = 0.

Phương pháp:
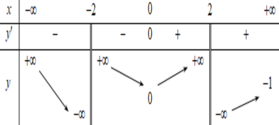
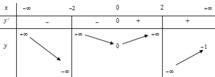
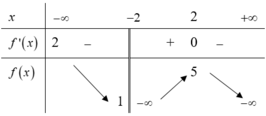
Quan sát đồ thị hàm số đã cho và dựa vào những kiến thức đã học về đồ thị hàm số để kết luận.
Cách giải:
Dựa vào BBT ta thấy đồ thị hàm số có tiệm cận đứng x=22 và tiệm cận ngang y=2
Chọn B.

Đáp án: A.
Nhận xét rằng hàm số dạng 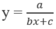 (a, b
≠
0) có tiệm cận đứng là
(a, b
≠
0) có tiệm cận đứng là 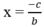 và tiệm cận ngang là y = 0.
và tiệm cận ngang là y = 0.


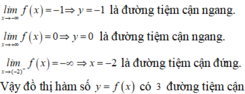


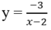
Chọn C
Dựa vào định nghĩa mệnh đề 1 sai và mệnh đề 2, 3, 4 đúng.