Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. có góc B cộng góc C bằng 180 độ ( tiế vậy nó nội tip tuyến ĐT) vậy nó nội tiếp
2. xét 2 tam giác ABE và tam giác AFB chứng minh nó đồng dạng (g,g), vì góc A chung, góc F bằng góc ABE = 1/2 Sđ cung BE. rồi lập tì số đồng dạng là được.
3. Chưa làm được. nếu bạn làm được rối thông tin cho mình nhé. cảm ơn

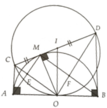
a, Dễ thấy A M B ^ = 90 0 hay E M F ^ = 90 0 tiếp tuyến CM,CA
=> OC ⊥ AM => O E M ^ = 90 0 Tương tự => O F M ^ = 90 0
Chứng minh được ∆CAO = ∆CMO => A O C ^ = M O C ^
=> OC là tia phân giác của A M O ^
Tương tự OD là tia phân giác của B O M ^ suy ra OC ⊥ OD <=> C O D ^
b, Do ∆AOM cân tại O nên OE là đường phân giác đồng thời là đường cao
=> O E M ^ = 90 0 chứng minh tương tự O F M ^ = 90 0
Vậy MEOF là hình chữ nhật
c, Gọi I là trung điểm CD thì I là tâm đường tròn đường kính CD và IO=IC=ID. Có ABDC là hình thang vuông tại A và B nên IO//AC//BD và IO vuông góc với AB. Do đó AB là tiếp tuyến của đường tròn đường kính CD.

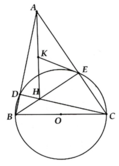
a, HS tự chứng minh
b, HS tự chứng minh
c, DAEH vuông nên ta có: KE = KA = 1 2 AH
=> DAKE cân tại K
=> K A E ^ = K E A ^
DEOC cân ở O => O C E ^ = O E C ^
H là trực tâm => AH ^ BC
Có A E K ^ + O E C ^ = H A C ^ + A C O ^ = 90 0
(K tâm ngoại tiếp) => OE ^ KE
d, HS tự làm

a) Tam giác ABC nội tiếp đường tròn (O) đường kính BC
=> OA=OB=OC và O là trung điểm của BC
=> Tam giác ABC vuông tại A
=> góc BAC = 90 độ
b) DO tam giác HAK nội tiếp đường tròn (I)
Lại có góc HAK = 90 độ
=> HK là đường kính của (I)
=> HK đi qua I
=> H,I,K thẳng hàng
c) Đề bài ghi ko rõ
d) 3 điểm nào?

B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)


a: Xét tứ giác BOCE có \(\widehat{EBO}+\widehat{ECO}=90^0+90^0=180^0\)
nên BOCE là tứ giác nội tiếp đường tròn đường kính EO
Tâm là trung điểm của EO
Bán kính là EO/2
b: Xét (O) có
DA,DC là các tiếp tuyến
Do đó: DA=DC
=>D nằm trên đường trung trực của AC
Xét (O) có
DA,DC là các tiếp tuyến
Do đó: OD là phân giác của góc AOC
=>\(\widehat{AOC}=2\cdot\widehat{COD}\)
Xét (O) có
EC,EB là các tiếp tuyến
Do đó: OE là phân giác của góc COB
=>\(\widehat{COB}=2\cdot\widehat{COE}\)
Xét (O) có
EC,EB là các tiếp tuyến
Do đó: EC=EB
Ta có: \(\widehat{COA}+\widehat{COB}=180^0\)
=>\(2\cdot\left(\widehat{COD}+\widehat{COE}\right)=180^0\)
=>\(2\cdot\widehat{DOE}=180^0\)
=>\(\widehat{DOE}=90^0\)
Xét ΔDOE vuông tại O có OC là đường cao
nên \(CD\cdot CE=OC^2\)
mà CD=DA và CE=EB
nên \(DA\cdot EB=OC^2\)
=>\(4\cdot DA\cdot EB=4\cdot OC^2=\left(2\cdot OC\right)^2=AB^2\)