Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

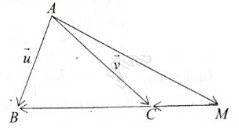
Ta có: \(\overrightarrow{MB}=3\overrightarrow{MC}\Rightarrow\overrightarrow{MB}=3\left(\overrightarrow{MB}+\overrightarrow{BC}\right)\)
\(\Rightarrow\overrightarrow{MB}=3\overrightarrow{MB}+3\overrightarrow{BC}\)
\(\Rightarrow-\overrightarrow{MB}=3\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{BM}=\dfrac{2}{3}\overrightarrow{BC}\). Mà \(\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}\) nên \(\overrightarrow{BM}=\dfrac{2}{3}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)
Theo quy tắc 3 điểm, ta có
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\Rightarrow\overrightarrow{AM}=\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}-\dfrac{3}{2}\overrightarrow{AB}\)
\(\Rightarrow\overrightarrow{AM}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}\) hay \(\overrightarrow{AM}=-\dfrac{1}{2}\overrightarrow{u}+\dfrac{3}{2}\overrightarrow{v}\)

a/ \(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{AE}+\overrightarrow{ED}+\overrightarrow{BF}+\overrightarrow{FE}+\overrightarrow{CD}+\overrightarrow{DF}\)
\(=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}+\overrightarrow{ED}+\overrightarrow{DF}+\overrightarrow{FE}\)
\(=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}+\overrightarrow{EF}+\overrightarrow{FE}\)
\(=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}\)
b/ Theo tính chất trung tuyến:
\(\left\{{}\begin{matrix}\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AK}\\\overrightarrow{BA}+\overrightarrow{BC}=2\overrightarrow{BM}\end{matrix}\right.\) \(\Rightarrow\overrightarrow{AC}+\overrightarrow{BC}=2\overrightarrow{AK}+2\overrightarrow{BM}\)
\(\overrightarrow{AC}=\overrightarrow{AK}+\overrightarrow{KC}=\overrightarrow{AK}+\frac{1}{2}\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{BC}=\overrightarrow{AK}+2\overrightarrow{BM}-\frac{1}{2}\overrightarrow{BC}\Rightarrow\overrightarrow{BC}=\frac{2}{3}\overrightarrow{AK}+\frac{4}{3}\overrightarrow{BM}\)
\(\Rightarrow\overrightarrow{AC}=\overrightarrow{AK}+\frac{1}{2}\left(\frac{3}{2}\overrightarrow{AK}+\frac{4}{3}\overrightarrow{BM}\right)=...\)
\(\overrightarrow{AB}=\overrightarrow{AC}-\overrightarrow{BC}=...\)

a/ \(\overrightarrow{DA}-\overrightarrow{DB}=\overrightarrow{DA}+\overrightarrow{BD}=\overrightarrow{BA}\)
\(\overrightarrow{OD}-\overrightarrow{OC}=\overrightarrow{OD}+\overrightarrow{CO}=\overrightarrow{CD}\)
Mà \(\overrightarrow{BA}=\overrightarrow{CD}\) (t/c hình bình hành) \(\Rightarrow\) đpcm
b/ Theo tính chất trung tuyến:
\(\left\{{}\begin{matrix}\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AK}\\\overrightarrow{BA}+\overrightarrow{BC}=2\overrightarrow{BM}\end{matrix}\right.\) \(\Rightarrow\overrightarrow{AC}+\overrightarrow{BC}=2\overrightarrow{AK}+2\overrightarrow{BM}\)
\(\Rightarrow\overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{AC}=2\overrightarrow{AK}+2\overrightarrow{BM}\)
\(\Rightarrow2\overrightarrow{AC}-\overrightarrow{AB}=2\overrightarrow{AK}+2\overrightarrow{BM}\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AK}\\2\overrightarrow{AC}-\overrightarrow{AB}=2\overrightarrow{AK}+2\overrightarrow{BM}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AC}=\frac{4}{3}\overrightarrow{AK}+\frac{2}{3}\overrightarrow{BM}\\\overrightarrow{AB}=\frac{2}{3}\overrightarrow{AK}-\frac{2}{3}\overrightarrow{BM}\end{matrix}\right.\)

A B C D E
Theo tính chất trung điểm
\(\overrightarrow{AE}=\dfrac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{AC}\right)=\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AC}\)\(=\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BC}\right)\)\(=\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)=\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AB}=\overrightarrow{u}+\dfrac{1}{2}\overrightarrow{v}\).

A B C M N K
Theo các xác định điểm M, N ta có:
\(\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB};\overrightarrow{AN}=\dfrac{2}{3}\overrightarrow{AC}.\)
Theo tính chất trung điểm của MN ta có:
\(\overrightarrow{AK}=\dfrac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=\dfrac{1}{2}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\right)\)
\(=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\).

TenAnh1
TenAnh1
A = (-4.3, -5.94)
A = (-4.3, -5.94)
A = (-4.3, -5.94)
B = (11.06, -5.94)
B = (11.06, -5.94)
B = (11.06, -5.94)
D = (10.84, -5.94)
D = (10.84, -5.94)
D = (10.84, -5.94)
a)
\(\overrightarrow{AO}=\overrightarrow{AB}+\overrightarrow{BO}=\overrightarrow{AB}+\overrightarrow{AF}\).
Vậy \(\overrightarrow{AD}=2\overrightarrow{AO}=2\left(\overrightarrow{AB}+\overrightarrow{AF}\right)\).
b)
\(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BC}\right)=\dfrac{1}{2}\overrightarrow{AC}\).
Vì vậy: \(\left|\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}\right|=\left|\dfrac{1}{2}\overrightarrow{AC}\right|=\dfrac{1}{2}AC\).
A B C a H
Do tam giác ABC cân tại B nên BH là đường cao, đường trung tuyến, đường phân giác ứng với đỉnh B của tam giác ABC.
Áp dụng hệ thức lượng trong tam giác vuông ta có:
\(AH=AB.sin60^o=\dfrac{a\sqrt{3}}{2}\).
\(AC=2BH=2.\dfrac{a\sqrt{3}}{2}=a\sqrt{3}\).
Vì vậy: \(\left|\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}\right|=\left|\dfrac{1}{2}\overrightarrow{AC}\right|=\dfrac{1}{2}AC\)\(=a\sqrt{3}\).

a) \(\overrightarrow{a}+\overrightarrow{b}=\left(2;-2\right)+\left(1;4\right)=\left(3;2\right)\).
\(\overrightarrow{a}-\overrightarrow{b}=\left(2;-2\right)-\left(1;4\right)=\left(1;-6\right)\).
\(2\overrightarrow{a}+3\overrightarrow{b}=2\left(2;-2\right)+3\left(1;4\right)=\left(4;-4\right)+\left(3;12\right)\)\(=\left(7;8\right)\).
c) Gọi x và y là hai số thực để:
\(\overrightarrow{c}=x\overrightarrow{a}+y\overrightarrow{b}=x\left(2;-2\right)+y\left(1;4\right)=\left(2x+y;-2x+4y\right)\)
Từ đó suy ra: \(\left\{{}\begin{matrix}2x+y=5\\-2x+4y=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\).
Vậy \(\overrightarrow{c}=2\overrightarrow{a}+1\overrightarrow{b}\).

Theo giả thiết ta có :
\(\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\left(\overrightarrow{AB}+\overrightarrow{CA}\right)=0\)
\(\Leftrightarrow\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\left(\overrightarrow{AB}-\overrightarrow{AC}\right)=0\)
\(\Leftrightarrow\overrightarrow{AB}^2-\overrightarrow{AC}^2=0\)
Ta suy ra ABC là tam giác có \(AB=AC\) (Tam giác cân tại A)
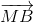 = 3
= 3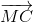 =>
=> 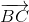 )
)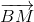 =
= 
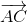 -
- 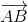 nên
nên 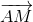 =
= 
Gọi G là giao điểm của AK, BM thì G là trọng tâm của tam giác.
Ta có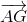 =
= 
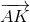 =>
=> 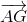 =
=

Theo quy tắc 3 điểm đối với tổng vec tơ:
AK là trung tuyến thuộc cạnh BC nên