Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M N Q P O R S T A B C H M D I A B C D K G M K E P F (Hình a) (Hình b) (Hình c) Q I
Bài toán 1: (Hình a)
Gọi đường thẳng qua N vuông góc với AN cắt AC tại R, qua P kẻ đường thẳng song song với BC. Đường thẳng này cắt AM,AN,BC lần lượt tại S,T,K.
Ta thấy \(\Delta\)APR có AN vừa là đường cao, đường phân giác => \(\Delta\)APR cân tại A => AP = AR, NP = NR
Áp dụng hệ quả ĐL Thales \(\frac{BM}{PS}=\frac{CM}{KS}\left(=\frac{AM}{AS}\right)\)=> PS = KS
Áp dụng ĐL đường phân giác trong tam giác: \(\frac{TK}{TP}=\frac{AK}{AP}\Rightarrow\frac{ST+SK}{TP}=\frac{AK}{AR}\)
\(\Rightarrow\frac{2ST+PT}{TP}=\frac{AR+RK}{AR}\Rightarrow\frac{2ST}{TP}=\frac{RK}{AR}\)
Dễ thấy NS là đường trung bình của \(\Delta\)RKP => RK = 2NS. Do đó \(\frac{ST}{TP}=\frac{NS}{AR}\)
Đồng thời NS // AR, suy ra \(\frac{ST}{TP}=\frac{NS}{AR}=\frac{SQ}{QA}\)=> QT // AP (ĐL Thaels đảo)
Mà AP vuông góc PO nên QT vuông góc PO. Từ đây suy ra T là trực tâm của \(\Delta\)POQ
=> QO vuông góc PT. Lại có PT // BC nên QO vuông góc BC (đpcm).
Bài toán 2: (Hình b)
Ta có IB = IC => \(\Delta\)BIC cân tại I => ^IBC = ^ICB = ^ACB/2 => \(\Delta\)MCI ~ \(\Delta\)MBC (g.g)
=> MC2 = MI.MB. Xét \(\Delta\)AHC có ^AHC = 900 , trung tuyến HM => HM = MC
Do đó MH2 = MI.MB => \(\Delta\)MIH ~ \(\Delta\)MHB (c.g.c) => ^MHI = ^MBH = ^MBC = ^MCI
=> Tứ giác CHIM nội tiếp. Mà CI là phân giác ^MCH nên (IH = (IM hay IM = IH (đpcm).
Bài toán 3: (Hình c)
a) Gọi đường thẳng qua C vuông góc CB cắt MK tại F, DE cắt BC tại Q, CG cắt BD tại I.
Áp dụng ĐL Melelaus:\(\frac{MB}{MC}.\frac{GA}{GB}.\frac{DC}{DA}=1\)suy ra \(\frac{DC}{DA}=2\)=> A là trung điểm DC
Khi đó G là trọng tâm của \(\Delta\)BCD. Do CG cắt BD tại I nên I là trung điểm BD
Dễ thấy \(\Delta\)BCD vuông cân tại B => BI = CM (=BC/2). Từ đó \(\Delta\)IBC = \(\Delta\)MCF (g.c.g)
=> CB = CF => \(\Delta\)BCF vuông cân ở C => ^CBA = ^CBF (=450) => B,A,F thẳng hàng
=> CA vuông góc GF. Từ đó K là trực tâm của \(\Delta\)CGF => GK vuông góc CF => GK // CM
Theo bổ đề hình thang thì P,Q lần lượt là trung điểm GK,CM. Kết hợp \(\Delta\)CEM vuông ở E
=> EQ=CM/2. Áp dụng ĐL Melelaus có \(\frac{GD}{GM}.\frac{EQ}{ED}.\frac{CM}{CQ}=1\)=> \(\frac{EQ}{ED}=\frac{1}{4}\)
=> \(\frac{ED}{CM}=2\)=> DE = 2CM = BC (đpcm).
b) Theo câu a thì EQ là trung tuyến của \(\Delta\)CEM vuông tại E => EQ = QC => ^QEC = ^QCE
Vì vậy ^PEG = ^QEC = ^QCE = ^PGE => \(\Delta\)EPG cân tại P => PG = PE (đpcm).

Giải
a) D thuộc đường trung trực của AB nên DA = DB (tính chất đường trung trực)
Vậy ∆ADB cân tại D.
E thuộc đường trung trực của AC nên AE = EC (tính chất đường trung trực)
Vậy ∆AEC cân tại A.
b)Vì O là giao điểm ba đường trung trực của ∆ABC nên:
OA = OB = OC
Vậy (O;OA) đi qua ba điểm A, B, C.
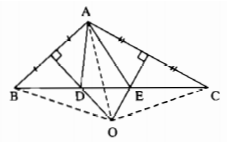
a: Ta có: \(\hat{BAE}+\hat{CAE}=\hat{BAC}=90^0\)
\(\hat{BEA}+\hat{HAE}=90^0\) (ΔEHA vuông tại H)
mà \(\hat{CAE}=\hat{HAE}\) (AE là phân giác của góc HAC)
nên \(\hat{BAE}=\hat{BEA}\)
=>ΔBAE cân tại B
Ta có: \(\hat{CAD}+\hat{BAD}=\hat{BAC}=90^0\)
\(\hat{CDA}+\hat{HAD}=90^0\) (ΔHAD vuông tại H)
mà \(\hat{BAD}=\hat{HAD}\) (AD là phân giác của góc BAH)
nên \(\hat{CAD}=\hat{CDA}\)
=>ΔCAD cân tại C
O là giao điểm của các đường phân giác trong ΔABC
=>BO là phân giác của góc ABE, CO là phân giác của góc ACD
Xét ΔBAE cân tại B có BO là đường phân giác
nên BO là đường trung trực của AE
=>OA=OE
Xét ΔCAD cân tại C có CO là đường phân giác
nên CO là đường trung trực của AD
=>OA=OD
=>OA=OE=OD
=>(O;OA) đi qua ba điểm A,D,E
b: Ta có: AD là phân giác của góc HAB
=>\(\hat{HAD}=\frac12\cdot\hat{HAB}\)
Ta có: AE là phân giác của góc HAC
=>\(\hat{HAE}=\frac12\cdot\hat{HAC}\)
Ta có: tia AH nằm giữa hai tia AE và AD
=>\(\hat{EAD}=\hat{EAH}+\hat{DAH}=\frac12\cdot\left(\hat{BAH}+\hat{CAH}\right)=\frac12\cdot\hat{BAC}=45^0\)
Xét (O;OE) có
\(\hat{EAD}\) là góc nội tiếp chắn cung ED
=>\(\hat{EOD}=2\cdot\hat{EAD}=2\cdot45^0=90^0\)
Câu a. Chứng minh A, D, E cùng thuộc (O; OA)
Ta phân tích:
👉 Điều cần chứng minh: D, E cũng nằm trên đường tròn này.
=> D nằm trên đường tròn (O; OA).
Kết luận: Đường tròn (O; OA) đi qua A, D, E. ✅
Câu b. Tính số đo ∠DOE
Ta biết:
👉 Suy nghĩ: ∠DOE sẽ liên quan đến ∠BAC.
Cách khác:
Trong đường tròn (O; OA):
✅ Kết quả:
a) (O; OA) đi qua A, D, E.
b) ∠DOE = 90°.
tham khảo