Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3:
\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
HB=12^2/20=7,2cm
=>HC=20-7,2=12,8cm
\(AD=\dfrac{2\cdot12\cdot16}{12+16}\cdot cos45=\dfrac{48\sqrt{2}}{7}\)
\(HD=\sqrt{AD^2-AH^2}=\dfrac{48}{35}\left(cm\right)\)

a) Ta thấy: \(AB.AC=BC.AH\)
\(\Leftrightarrow AB^2.AC^2=BC^2.AH^2\)
\(\Leftrightarrow AH^2=\frac{AB^2.AC^2}{BC^2}\)
\(\Leftrightarrow AH^2=\frac{AB^2.AC^2}{AB^2+AC^2}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{AB^2+AC^2}{AB^2.AC^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
Ta có: \(\frac{AB}{AC}=\frac{5}{7}\Rightarrow AB:AC=\frac{5}{7}\Rightarrow AB=\frac{5}{7}AC\)
Áp dụng công thức trên: \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{15^2}=\frac{1}{\frac{25}{49}AC^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{225}=\frac{49}{25}.\frac{1}{AC^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{225}=\frac{1}{AC^2}\left(\frac{49}{25}+1\right)\)
\(\Rightarrow\frac{1}{225}=\frac{1}{AC^2}.\frac{74}{25}\Rightarrow\frac{1}{AC^2}=\frac{1}{225}.\frac{25}{74}=\frac{1}{666}\Rightarrow AC^2=666\Rightarrow AC=\sqrt{666}=3\sqrt{74}cm\)
Do đó: \(AB=\frac{5}{7}.3\sqrt{74}=\frac{15\sqrt{74}}{7}cm\)
Xét tam giác ABH có: \(AH^2+BH^2=AB^2\Leftrightarrow15^2+BH^2=\left(\frac{15\sqrt{74}}{7}\right)^2\Leftrightarrow BH^2=\frac{16650}{49}-225=\frac{5625}{49}\)
\(\Rightarrow BH=\frac{\sqrt{5625}}{\sqrt{49}}=\frac{75}{7}cm\)
Xét tam giác ACH có: \(AH^2+HC^2=AC^2\Leftrightarrow15^2+HC^2=666\Leftrightarrow HC^2=666-225=441\)
\(\Rightarrow HC=\sqrt{441}=21cm\)
Vậy: \(BH=\frac{75}{7}cm\) và \(HC=21cm\)
b) Chu vi tam giác ABC là: \(AB+AC+BC=\frac{15\sqrt{74}}{7}+3\sqrt{74}+21+\frac{75}{7}\approx76cm\)
A B C H 15 cm
Vì tam giác ABC vuông tại A => góc B + góc C = 90o
Vì tam giác HAC vuông tại H => góc HAC + góc C = 90o
=> góc HAC = góc B
Xét tam giác HAC và tam giác HBA có:
góc HAC = góc B (cmt)
góc AHC = góc AHB (=90o)
=> tam giác HAC đồng dạng với tam giác HBA (TH3)
=> \(\frac{AC}{AB}=\frac{AH}{BH}=\frac{HC}{AH}=\frac{7}{5}\)
=> \(HC=15.\frac{7}{5}=21\left(cm\right);HB=15.\frac{5}{7}=\frac{75}{7}\left(cm\right)\)
Sau đó tính AB; AC; BC. Ngại là lắm, làm nốt nhá ._.

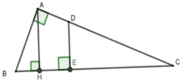
Gọi D là giao điểm của AC và đường vuông góc với BC tại E.
Xét ΔAHC và ΔABC có C chung và A H C ^ = B A C ^ = 90 ∘ nên ΔAHC ~ ΔBAC (g-g)
Ta có S D E C = 1 2 S A B C (1), S A H C : S A B C = 18 25 (2).
Từ (1) và (2) suy ra
S D E C : S A H C = 1 2 : 18 25 = 25 36 = ( 5 6 ) 2 3
Vì DE // AH (cùng vuông với BC) duy ra ΔDEC ~ ΔAHC nên
S D E C : S A H C = ( E C H C ) 2 (4)
Từ (3) và (4) suy ra E C H C = 5 6 tức là E C 18 = 5 6 => EC = 15cm.
Đáp án: A

a, Vì IK là đtb tg AHB nên IK//AB hay IK⊥AC (AB⊥AC)
Xét tg AKC có AH là đg cao (AH⊥BC), IK là đg cao (IK⊥AC), AH cắt IK tại I nên I là trực tâm
Do đó CI là đg cao còn lại
Vậy CI⊥AK

△ABH∼△CAH (g-g) \(\Rightarrow\dfrac{P_{ABH}}{P_{CAH}}=\dfrac{AB}{CA}=\dfrac{18}{24}=\dfrac{3}{4}\)
\(\Rightarrow AB=\dfrac{3}{4}CA\)
△ABC vuông tại A có: \(BC^2=AB^2+AC^2\Rightarrow BC^2=\dfrac{9}{16}CA^2+CA^2=\dfrac{25}{16}CA^2\)
\(\Rightarrow BC=\dfrac{5}{4}CA\)
△CAH∼△CBA (g-g) \(\Rightarrow\dfrac{P_{CAH}}{P_{CBA}}=\dfrac{CA}{CB}=\dfrac{CA}{\dfrac{5}{4}CA}=\dfrac{4}{5}\)
\(\Rightarrow P_{CBA}=\dfrac{5}{4}.P_{CAH}=\dfrac{5}{4}.24=30\left(cm\right)\)
\(AH=\sqrt{HB\cdot HC}=24\left(cm\right)\)
BC=BH+CH=50(cm)
\(AB=\sqrt{18^2+24^2}=30\left(cm\right)\)
\(AC=\sqrt{24^2+32^2}=40\left(cm\right)\)
C=50+30+40=120(cm)