Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) =
=
b) =
=
=
. ( Với điều kiện b # 1)
c) \(\dfrac{a^{\dfrac{1}{3}}b^{-\dfrac{1}{3}-}a^{-\dfrac{1}{3}}b^{\dfrac{1}{3}}}{\sqrt[3]{a^2}-\sqrt[3]{b^2}}\)= =
=
( với điều kiện a#b).
d) \(\dfrac{a^{\dfrac{1}{3}}\sqrt{b}+b^{\dfrac{1}{3}}\sqrt{a}}{\sqrt[6]{a}+\sqrt[6]{b}}\) = =
=
=

a) ta có 2√5= = √20 ; 3√2 =
= √ 18 => 2√5 > 3√2
=> <
b) 6√3 = = √108 ; 3√6 =
= √54 => 6√3 > 3√6 =>
>
a) \(2\sqrt{5}=\sqrt{2^2.5}=\sqrt{20}\)
\(3\sqrt{2}=\sqrt{3^2.2}=\sqrt{18}\)
=> \(2\sqrt{5}>3\sqrt{2}\)
=> \(\left(\dfrac{1}{3}\right)^{2\sqrt{5}}< \left(\dfrac{1}{3}\right)^{3\sqrt{2}}\)
(vì cơ số \(\dfrac{1}{3}< 1\))
b) Vì \(3< 6^2\)
=> \(3^{\dfrac{1}{6}}< \left(6^2\right)^{\dfrac{1}{6}}\)
=> \(\sqrt[6]{3}< 6^{\dfrac{1}{3}}\)
=> \(\sqrt[6]{3}< \sqrt[3]{6}\)
=> \(7^{\sqrt[6]{3}}< 7^{\sqrt[3]{6}}\)

a)
\(A=\dfrac{a^{\dfrac{4}{3}}\left(a^{-\dfrac{1}{3}}+a^{\dfrac{2}{3}}\right)}{a^{\dfrac{1}{4}}\left(a^{\dfrac{3}{4}}+a^{-\dfrac{1}{4}}\right)}=\dfrac{a^{\left(\dfrac{4}{3}-\dfrac{1}{3}\right)+}a^{\left(\dfrac{4}{3}+\dfrac{2}{3}\right)}}{a^{\left(\dfrac{1}{4}+\dfrac{3}{4}\right)}+a^{\left(\dfrac{1}{4}-\dfrac{1}{4}\right)}}=\dfrac{a+a^2}{a+1}=\dfrac{a\left(a+1\right)}{a+1}\)
\(a>0\Rightarrow a+1\ne0\) \(\Rightarrow A=a\)

Lời giải:
Từ $A$ kẻ $AA'$ song song với trục $OO'$ ( $A'$ nằm trên đáy có tâm $O'$)
Khi đó \(AA'=OO'=a\sqrt{3}\) và \(AA'\) vuông góc với hai đáy.
\(AA'\parallel OO'\Rightarrow OO'\parallel (AA'B)\)
\(\Rightarrow d(OO', AB)=d(OO', (AA'B))=d(O', (AA'B))\)
Kẻ \(O'H\perp A'B\)
\(\left\{\begin{matrix} O'H\subset (\text{ đáy})\rightarrow O'H\perp AA'\\ O'H\perp A'B \end{matrix}\right.\) \(\Rightarrow O'H\perp (AA'B)\)
\(\Rightarrow O'H=d(O', (AA'B))=d(OO', AB)\)
-------------------------------------------
Do \(OO'\parallel AA'\) nên:
\((OO', AB)=30^0\Rightarrow (AA', AB)=30^0\Leftrightarrow \angle BAA'=30^0\)
\(\Rightarrow \frac{\sqrt{3}}{3}=\tan BAA'=\frac{BA'}{AA}=\frac{BA'}{a\sqrt{3}}\)
\(\Rightarrow BA'=a\Rightarrow BH=\frac{a}{2}\)
\(O'H=\sqrt{O'B^2-BH^2}=\sqrt{r^2-BH^2}=\sqrt{a^2-(\frac{a}{2})^2}=\frac{\sqrt{3}}{2}a\)
\(\Leftrightarrow d(AB,OO')=\frac{\sqrt{3}}{2}a\)
Đáp án B

a) .
=
=
=
=
= 9.
b) :
=
=
=
=
=
= 8.
c) +
=
+
=
+
=
+
=
+
= 40.
d) -
=
-
=
-
=
-
= 121.
a) \(9^{\dfrac{2}{5}}.27^{\dfrac{2}{5}}=\left(9.27\right)^{\dfrac{2}{5}}=\left(3^2.3^3\right)^{\dfrac{2}{5}}=3^{5.\dfrac{2}{5}}=3^2=9\)
b) \(=\left(\dfrac{144}{9}\right)^{\dfrac{3}{4}}=\left(\dfrac{12}{3}\right)^{2.\dfrac{3}{4}}=4^{\dfrac{3}{2}}=2^{2.\dfrac{3}{2}}=2^3=8\)
c) \(=\left(\dfrac{1}{2}\right)^{4.\left(-0,75\right)}+\left(\dfrac{1}{4}\right)^{-\dfrac{5}{2}}\)
\(=\left(\dfrac{1}{2}\right)^{-3}+\left(\dfrac{1}{2}\right)^{-5}\)
\(=2^3+2^5=40\)
d) \(=\left(0,2\right)^{2.\left(-1.5\right)}-\left(0,5\right)^{3.\dfrac{-2}{3}}\)
\(=\left(\dfrac{1}{5}\right)^{-3}-\left(\dfrac{1}{2}\right)^{-2}\)
\(=5^3-2^2=121\)

- Xét a = 0 hàm số trở thành y = -9x + b. Trường hợp này hàm số không có cực trị.
- Xét a # 0. Ta có : y’ = 5a2x2 + 4ax – 9 ; y’= 0 ⇔ hoặc
- Với a < 0 ta có bảng biến thiên :
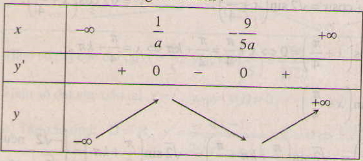
Theo giả thiết là điểm cực đại nên
. Theo yêu cầu bài toán thì
- Với a > 0 ta có bảng biến thiên :
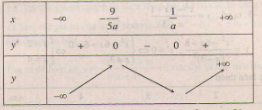
Vì là điểm cực đại nên
. Theo yêu cầu bài toán thì:
Vậy các giá trị a, b cần tìm là: hoặc
.

Lời giải:
Đặt \(\log_yx=a,\log_xy=b\). Khi đó ta có:
\(\left\{\begin{matrix} a+b=\frac{10}{3}\\ ab=\log_xy.\log_yx=1\end{matrix}\right.\)
Áp dụng định lý Viete đảo thì \(a,b\) là nghiệm của PT:
\(x^2-\frac{10}{3}x+1=0\) . PT trên có hai nghiệm \(3,\frac{1}{3}\)
Giả sử \(a=\log_yx=3\) và \(b=\log_xy=\frac{1}{3}\)
\(\left\{\begin{matrix} \log_y\left(\frac{144}{y}\right)=3\\ \log_x\left(\frac{144}{x}\right)=\frac{1}{3} \end{matrix}\right.\Rightarrow \left\{\begin{matrix} x=24\sqrt{3}\\ y=2\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow \frac{x+y}{2}=13\sqrt{3}\). Đáp án D
2.
a)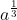 .
. 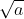 =
= 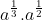 =
= 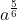 .
.
b)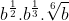 =
= 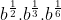 =
=  = b.
= b.
c)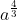 :
: 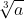 =
= 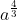 :
: 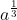 = a.
= a.
d)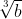 :
: 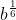 =
= 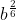 :
: 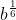 =
= 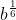
Câu a, b thì Nguyễn Quang Duy làm đúng rồi.
c) \(a^{\dfrac{4}{3}}:\sqrt[3]{a}=a^{\dfrac{4}{3}}:a^{\dfrac{1}{3}}=a^{\dfrac{4}{3}-\dfrac{1}{3}}=a\)
d) \(\sqrt[3]{b}:b^{\dfrac{1}{6}}=b^{\dfrac{1}{3}}:b^{\dfrac{1}{6}}=b^{\dfrac{1}{3}-\dfrac{1}{6}}=b^{\dfrac{1}{6}}\)