Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)

b) Phương trình hoành độ giao điểm của hai đường thẳng đã cho:
-3x + 5 = 2x
⇔ 2x + 3x = 5
⇔ 5x = 5
⇔ x = 1 ⇒ y = 2.1 = 2
Vậy M(1; 2)

a: 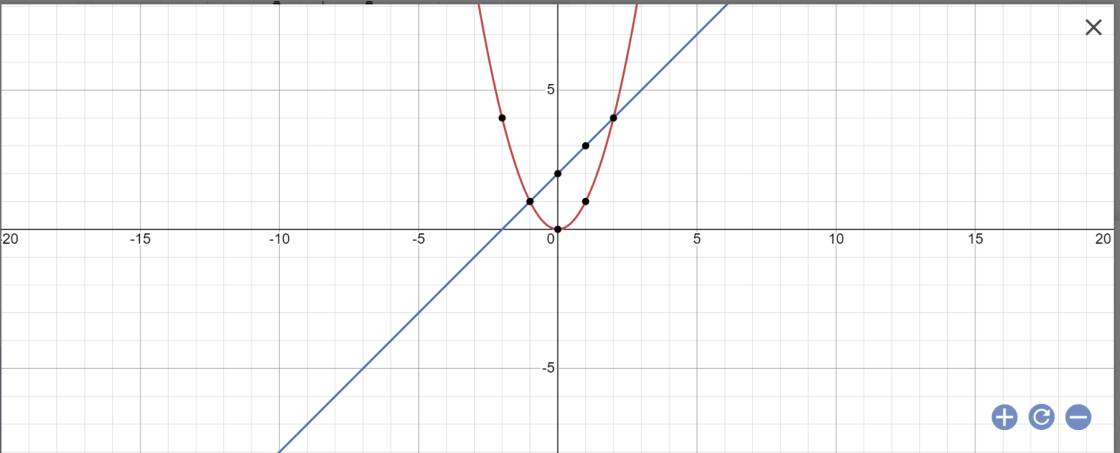
b: PTHĐGĐ là:
x^2-x-2=0
=>(x-2)(x+1)=0
=>x=2 hoặc x=-1
=>y=4 hoặc y=1
c: PTHĐGĐ là:
x^2-2x+m=0
Để (P) cắt (d1) tại hai điểm nằm về hai phía của trục tung thì m<0

a)Tự vẽ
b) Xét pt hoành độ gđ của (P) và (d) có:
\(\dfrac{3}{2}x^2=x+\dfrac{1}{2}\)
\(\Leftrightarrow3x^2-2x-1=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\Rightarrow y=\dfrac{3}{2}.\left(-\dfrac{1}{3}\right)^2=\dfrac{1}{6}\\x=1\Rightarrow y=\dfrac{3}{2}\end{matrix}\right.\)
Vậy gđ của (d) và (P) là \(\left(-\dfrac{1}{3};\dfrac{1}{6}\right),\left(1;\dfrac{3}{2}\right)\)
c) Gọi đt cần tìm có dạng (d') \(y=ax+b\) (a2+b2>0)
Gọi A(-4;y1) và B(2;y2) là hai giao điểm của (P) và (d')
\(A;B\in\left(P\right)\Rightarrow\left\{{}\begin{matrix}y_1=24\\y_2=6\end{matrix}\right.\)
\(\Rightarrow A\left(-4;24\right),B\left(2;6\right)\) \(\in\left(d'\right)\)
\(\Rightarrow\left\{{}\begin{matrix}24=-4a+b\\6=2a+b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=12\end{matrix}\right.\) (thỏa)
Vậy (d'): y=-3x+12

b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}3x^2-2x-1=0\\y=3x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x^2-3x+x-1=0\\y=3x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(3x+1\right)=0\\y=3x^2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(1;3\right);\left(-\dfrac{1}{3};\dfrac{1}{3}\right)\right\}\)

1. Cái này chắc bạn tự vẽ được nhỉ?
2.
a, -Gọi pt đường thẳng cần tìm là (d): y=ax+b (a\(\ne\)0)
- Vì A (\(\dfrac{-2}{3}\); -7) và B(2; 1) \(\in\) (d)
=> hệ pt: (1): -7= \(\dfrac{-2}{3}\)a+b
(2): 1= 2a+b
(bạn tự giải hệ nhé) => a= 3 (tmđk); b=-5
=> pt đường thẳng cần tìm: y=3x-5
b, - Xét pt hoành độ giao điểm của (P) và (d):
=> -2x\(^2\)=3x-5
=> x=1 hoặc x=-\(\dfrac{5}{2}\)
- Với C, D là hai giao điểm của (P) và (d):
+ Khi x=1 => y=-2 => C (1; -2)
+ Khi x=-\(\dfrac{5}{2}\) => y= -\(\dfrac{25}{2}\) => D (-\(\dfrac{5}{2}\); -\(\dfrac{25}{2}\))
3. - Để tổng hoành độ và tung độ của điểm cần tìm bằng 6
=> x+y=6
mà điểm đó thuộc (P) nên thay y= -2x\(^2\) vào pt, ta được:
x-2x\(^2\)=6 <=> -2x\(^2\)+x-6=0
=> vô nghiệm
=> không có điểm nào nằm trên (P) có tổng hoành độ và tung độ bằng 6



c: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x+3=x+1\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-1\end{matrix}\right.\)