K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 10 2023
d) \(\dfrac{1}{x^4y^6z};\dfrac{2}{3x^2y^7z^2};\dfrac{3}{4x^5y}\)
Mẫu thức chung: \(12x^5y^7z^2\)
Quy đồng mẫu thức các phân thức ta được:
\(\dfrac{12xyz}{12x^5y^7z^2};\dfrac{8x^3}{12x^5y^7z^2};\dfrac{9y^6z^2}{12x^5y^7z^2}\)
9 tháng 12 2023
c: \(\dfrac{2x}{x+5}+\dfrac{10x}{x^2+5x}\)
\(=\dfrac{2x}{x+5}+\dfrac{10x}{x\left(x+5\right)}\)
\(=\dfrac{2x}{x+5}+\dfrac{10}{x+5}=\dfrac{2x+10}{x+5}=\dfrac{2\left(x+5\right)}{x+5}=2\)
d: \(\dfrac{x}{x^2-36}+\dfrac{x-6}{x^2+6x}+\dfrac{-36}{\left(x^2-6x\right)\left(x+6\right)}\)
\(=\dfrac{x}{\left(x-6\right)\left(x+6\right)}+\dfrac{x-6}{x\left(x+6\right)}+\dfrac{-36}{x\left(x-6\right)\left(x+6\right)}\)
\(=\dfrac{x^2+\left(x-6\right)^2-36}{x\left(x-6\right)\left(x+6\right)}\)
\(=\dfrac{x^2+x^2-12x+36-36}{x\left(x-6\right)\left(x+6\right)}=\dfrac{2x^2-12x}{x\left(x-6\right)\left(x+6\right)}\)
\(=\dfrac{2\left(x^2-6x\right)}{\left(x^2-6x\right)\left(x+6\right)}=\dfrac{2}{x+6}\)
12 tháng 12 2016
a, Xét \(\Delta ABH\)và\(\Delta APE\)
Ta có: góc BHA = góc PEA (=90')
AH = AE ( cạnh của hình vuông AHKE)
góc BAH = góc PAE ( cùng bằng 90' trừ đi góc HAP)
Do đó \(\Delta ABH=\Delta APE\)(cạnh huyền - góc nhọn)
Suy ra: AB = AP
Suy ra: \(\Delta APB\)cân tại A.
12 tháng 12 2016
cảm ơn bạn nhiều nhé. nếu bạn biết làm 2 câu cuối thì có thể chỉ mình luôn đk ko ạ? mình cần gấp lắm
DD
0
29 tháng 10 2019
Ta có hcn AFCK =>
AK song song với FC và góc KAF = góc CFA =900(1)
=> Góc CAK = Góc KFC ( đồng vị) (2)
Ta có góc KAF = góc KAC+ góc CAF
góc CFA = góc CFK + góc KFA
Từ (1) và (2) => góc CAF = góc KFA
=> tam giác AEF là tam giác cân
=> AE = AF
Ta có tam giác ABC cân
=> góc B = góc C và AB = AC
Do D là trung điểm của AB, E là trung điểmm của AC
Mà AB = AC
Nên AD= DB = AE = EC
xét tam giác BDF và tam giác CEF có
góc B = góc C
BD = CE
BF = CF ( F là trung điểm của BC)
Nên tam giác BDF = tam giác CEF
=> góc DFB = góc EFC
Xét tam giác ABC cân tại A
Ta có À là đường trung tuyến
=> AF đồng thời là đường cao và đường phân giác
=> góc AFB = góc AFC = 900
=> góc BAF = góc CAF
Ta có góc AFB = góc AFD + góc DFB (3)
góc AFC = góc AFE + góc EFC (4)
theo cmt ta có góc DFB = góc EFC (5)
Từ (3) (4) (5) => góc DFA = góc EFA
Mà góc EFA = EAF ( tam giác EAF cân)
Góc EAF = góc DAF
nên góc DAF = góc DFA
=> tam giác DAF cân
=> DA = DF
Xét tứ giác ADFE có
AD = DF = AE = EF
Nên tứ giác ADFE là hình thoi ( theo dấu hiệu nhận biết)
Mình giải như thế cậu xem nhé
11 tháng 12 2023
b: ĐKXĐ: x<>-3
\(\dfrac{3x+x^2}{x^2+x+1}\cdot\dfrac{3x^3-3}{x+3}\)
\(=\dfrac{x\left(x+3\right)}{x^2+x+1}\cdot\dfrac{3\left(x^3-1\right)}{x+3}\)
\(=\dfrac{3x\left(x-1\right)\left(x^2+x+1\right)}{x^2+x+1}=3x\left(x-1\right)\)
e: ĐKXĐ: \(x\notin\left\{4;-5\right\}\)
\(\dfrac{2x+10}{x^3-64}:\dfrac{\left(x+5\right)^2}{2x-8}\)
\(=\dfrac{2\left(x+5\right)}{\left(x-4\right)\left(x^2+4x+16\right)}\cdot\dfrac{2x-8}{\left(x+5\right)^2}\)
\(=\dfrac{2\cdot2\left(x-4\right)}{\left(x-4\right)\left(x^2+4x+16\right)}=\dfrac{4}{x^2+4x+16}\)
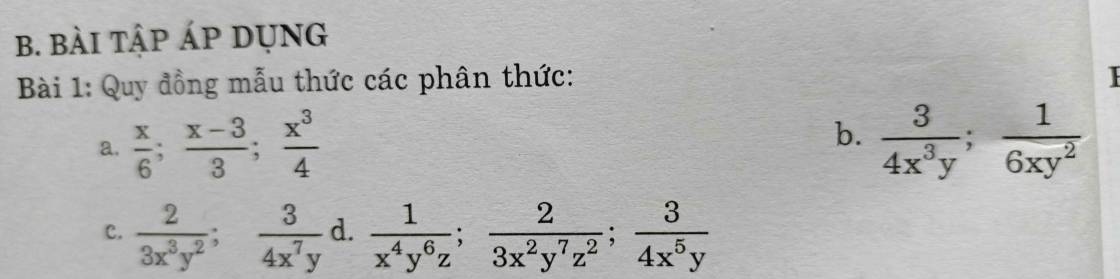
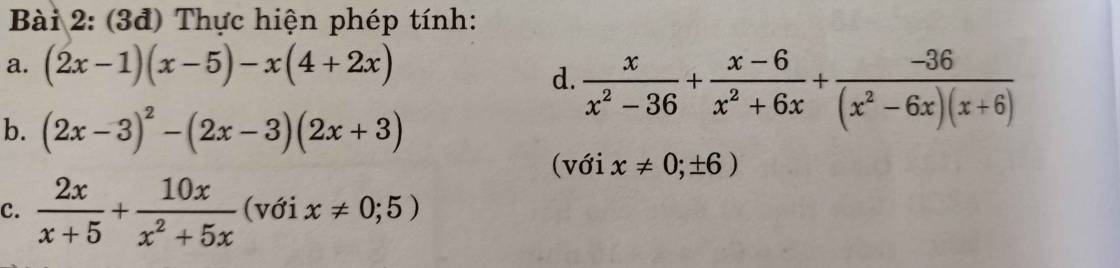
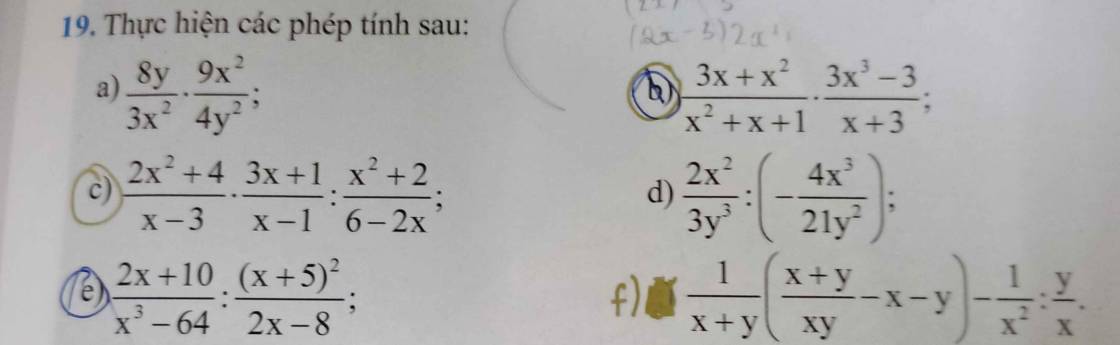
Chòi chòi, nhìn toán hình là hết ưa nổi