K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CT
Cô Tuyết Ngọc
Manager
VIP
28 tháng 3 2023
Hướng dẫn thí sinh tham gia thi thử trên OLM-ĐGNL: https://dgnl.olm.vn/tin-tuc/huong-dan-hoc-sinh-tham-gia-thi-thu-tren-olm-dgnl-643823112
KV
21 tháng 5 2023
4/7 : 2/5 = 10/7
Tổng số phần bằng nhau:
10 + 7 = 17 (phần)
Số sản phẩm cửa hàng thứ hai bán được:
1360 : 17 × 10 = 800 (sản phẩm)
Số sản phẩm cửa hàng thứ nhất bán được:
1360 : 17 × 7 = 560 (sản phẩm)
15 tháng 5 2023
Cậu đăng lên mục câu hỏi để mọi người có thể giúp cậu được nha!
AH
Akai Haruma
Giáo viên
30 tháng 9 2020
Bài 3:
Áp dụng các hằng đẳng thức đáng nhớ ta có:
$C=a^4+b^4=(a^2+b^2)^2-2a^2b^2$
$=[(a+b)^2-2ab]^2-2(ab)^2$
$=(8^2-2.15)^2-2.15^2=706$
AH
Akai Haruma
Giáo viên
30 tháng 9 2020
Bài 2:
a)
$D=-x^2+6x-11=-11-(x^2-6x)=-2-(x^2-6x+9)$
$=-2-(x-3)^2$
Vì $(x-3)^2\geq 0$ với mọi $x$ nên $D=-2-(x-3)^2\leq -2$
Vậy GTLN của $D$ là $-2$ khi $(x-3)^2=0\Leftrightarrow x=3$
b)
$F=4x-x^2+1=1-(x^2-4x)=5-(x^2-4x+4)=5-(x-2)^2$
$\leq 5-0=5$
Vậy $F_{\max}=5$. Giá trị này được khi $(x-2)^2=0\leftrightarrow x=2$
H
0
H
31 tháng 3 2017
a) y= -x4 + 2mx2 – 2m + 1(Cm). Tập xác định: D = R
y ‘ = -4x3 + 4mx = -4x (x2 – m)
- Với m ≤ 0 thì y’ có một nghiệm x = 0 và đổi dấu + sang – khi qua nghiệm này. Do đó hàm số có một cực đại là x = 0
Do đó, hàm số có 2 cực trị tại x = ± √m và có một cực tiểu tại x = 0
b) Phương trình -x4 + 2mx2 – 2m + 1 = 0 luôn có nghiệm x = ± 1 với mọi m nên (Cm) luôn cắt trục hoành.
c) Theo lời giải câu a, ta thấy ngay:
với m > 0 thì đồ thị (Cm) có cực đại và cực tiểu.
QD
31 tháng 3 2017
a) .
=
=
=
=
= 9.
b) :
=
=
=
=
=
= 8.
c) +
=
+
=
+
=
+
=
+
= 40.
d) -
=
-
=
-
=
-
= 121.
GV
Giáo viên Toán
Giáo viên
26 tháng 4 2017
a) \(9^{\dfrac{2}{5}}.27^{\dfrac{2}{5}}=\left(9.27\right)^{\dfrac{2}{5}}=\left(3^2.3^3\right)^{\dfrac{2}{5}}=3^{5.\dfrac{2}{5}}=3^2=9\)
b) \(=\left(\dfrac{144}{9}\right)^{\dfrac{3}{4}}=\left(\dfrac{12}{3}\right)^{2.\dfrac{3}{4}}=4^{\dfrac{3}{2}}=2^{2.\dfrac{3}{2}}=2^3=8\)
c) \(=\left(\dfrac{1}{2}\right)^{4.\left(-0,75\right)}+\left(\dfrac{1}{4}\right)^{-\dfrac{5}{2}}\)
\(=\left(\dfrac{1}{2}\right)^{-3}+\left(\dfrac{1}{2}\right)^{-5}\)
\(=2^3+2^5=40\)
d) \(=\left(0,2\right)^{2.\left(-1.5\right)}-\left(0,5\right)^{3.\dfrac{-2}{3}}\)
\(=\left(\dfrac{1}{5}\right)^{-3}-\left(\dfrac{1}{2}\right)^{-2}\)
\(=5^3-2^2=121\)
Q
31 tháng 3 2017
- Xét a = 0 hàm số trở thành y = -9x + b. Trường hợp này hàm số không có cực trị.
- Xét a # 0. Ta có : y’ = 5a2x2 + 4ax – 9 ; y’= 0 ⇔ hoặc
- Với a < 0 ta có bảng biến thiên :
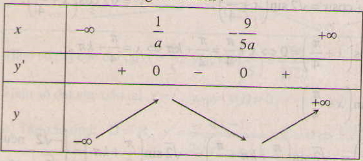
Theo giả thiết là điểm cực đại nên
. Theo yêu cầu bài toán thì
- Với a > 0 ta có bảng biến thiên :
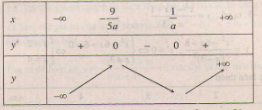
Vì là điểm cực đại nên
. Theo yêu cầu bài toán thì:
Vậy các giá trị a, b cần tìm là: hoặc
.
Q
7 tháng 6 2017
a) \(2^{x+4}+2^{x+2}=5^{x+1}+3\cdot5^x\)
\(\Rightarrow2^x+2^4+2x^x+2^2=5^x\cdot x+3\cdot5^x\)
\(\Leftrightarrow2^x+16+2^x\cdot4=5\cdot5^x+3\cdot5^x\)
\(\Leftrightarrow16\cdot2^x+4\cdot2^x=8\cdot5^x\)
\(\Leftrightarrow20\cdot2^x=8\cdot5^x\)
\(\Leftrightarrow20\cdot\left(\dfrac{2}{5}\right)^x=8\)
\(\Leftrightarrow\left(\dfrac{2}{5}\right)^x=\dfrac{2}{5}\)
\(\Leftrightarrow\left(\dfrac{2}{5}\right)^x=\left(\dfrac{2}{5}\right)^1\)
\(\Rightarrow x=1\)
QD
31 tháng 3 2017
a) ta có 2√5= = √20 ; 3√2 =
= √ 18 => 2√5 > 3√2
=> <
b) 6√3 = = √108 ; 3√6 =
= √54 => 6√3 > 3√6 =>
>
GV
Giáo viên Toán
Giáo viên
26 tháng 4 2017
a) \(2\sqrt{5}=\sqrt{2^2.5}=\sqrt{20}\)
\(3\sqrt{2}=\sqrt{3^2.2}=\sqrt{18}\)
=> \(2\sqrt{5}>3\sqrt{2}\)
=> \(\left(\dfrac{1}{3}\right)^{2\sqrt{5}}< \left(\dfrac{1}{3}\right)^{3\sqrt{2}}\)
(vì cơ số \(\dfrac{1}{3}< 1\))
b) Vì \(3< 6^2\)
=> \(3^{\dfrac{1}{6}}< \left(6^2\right)^{\dfrac{1}{6}}\)
=> \(\sqrt[6]{3}< 6^{\dfrac{1}{3}}\)
=> \(\sqrt[6]{3}< \sqrt[3]{6}\)
=> \(7^{\sqrt[6]{3}}< 7^{\sqrt[3]{6}}\)
Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!