Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
Cắt khối đa diện đã cho làm hai khối: khối lăng trụ và khối tứ diện.
Cách giải:
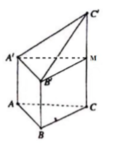
Gọi M là trung điểm của CC’.
Khi đó: khối đa diện đã cho được chia làm 2 phần: Khối lăng trụ tam giác đều A’B’M.ABC và khối tứ diện A’B’C’M.
Thể tích khối lăng trụ tam giác đều A’B’M.ABC là:

Đáp án A.
Gọi cạnh đáy của khối chóp là x với
0 < x < 5 2 2 .
Chiều cao của khối chóp là
h = 5 2 2 − x 2 2 − x 2 2 = 25 − 5 x 2 2 .
Vậy thể tích của khối chóp là
V = 1 3 . h . S = 1 3 . x 2 . 25 − 5 x 2 2 = 1 3 25 x 4 − 5 x 5 2 2 .
Xét hàm số f x = 25 x 4 − 5 x 5 2 trên 0 ; 5 2 2 ,
ta có f ' x = 100 x 3 − 25 x 4 2 = 0 ⇔ x = 2 2 .
Suy ra giá trị lớn nhất của thể tích là V = 1 3 . f 2 2 2 = 4 10 3 .

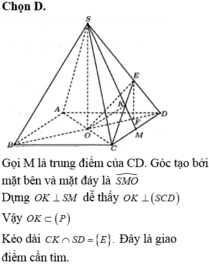
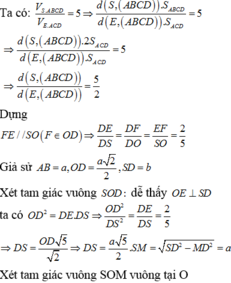
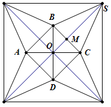

Chọn A