Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2/
Xét phân số \(\dfrac{2n-3}{n+1}=\dfrac{2n+2-5}{n+1}=\dfrac{2n+2}{n+1}-\dfrac{5}{n+1}=\dfrac{2\left(n+1\right)}{n+1}-\dfrac{5}{n+1}=2-\dfrac{5}{n+1}\)
\(n\in Z\Rightarrow2n-3\inƯ\left(5\right)=\left\{-1;-5;1;5\right\}\)
Ta có bảng:
| 2n - 3 | -1 | -5 | 1 | 5 |
| n | 1 | -1 | 2 | 4 |
Vậy \(n\in\left\{-1;1;2;4\right\}\)
1/
(x + 1) + (x + 3) + (x + 5) + ... + (x + 999) = 500
<=> (x + x + x + ... + x) + (1 + 3 + 5 + ... + 999) = 500
Xét tổng A = 1 + 3 + 5 + ... + 999
Số số hạng của A là: (999 - 1) : 2 + 1 = 500
Tổng A là: (999 + 1) x 500 : 2 = 250 000
Do A có 500 số hạng nên có 500 ẩn x.
Vậy ta có: 500x + 250 000 = 500
=> 500x = -249 500
=> x = 499
Vậy x = 499

a)
\(175\cdot19+38\cdot175+43\cdot175\\ =175\cdot19+175\cdot38+175\cdot43\\ =175\cdot\left(19+38+43\right)\\ =175\cdot100\\ =17500\)
b)
\(125\cdot75+125\cdot13-80\cdot125\\ =125\cdot75+125\cdot13-125\cdot80\\ =125\cdot\left(75+13-80\right)\\ =125\cdot10\\ =125\cdot8\\ =1000\)
a, 175. 19 + 38. 175 + 43. 175
= 175. 19 + 175. 38 + 175. 43
= 175.(19 + 38 + 43)
= 175. 100
= 17500


a) Có 18 học sinh đi đến trường bằng xe đạp.
b) Lớp 6A có 45 học sinh.
c) Tỉ số phần trăm học sinh đi bộ đến trường là:
(9 : 45) . 100 = 20%

bài 3:
a: \(C=5+5^2+5^3+\cdots+5^{20}\)
\(=5\left(1+5+5^2+\cdots+5^{19}\right)\) ⋮5
b: \(C=5+5^2+5^3+\cdots+5^{20}\)
\(=\left(5+5^2\right)+\left(5^3+5^4\right)+\cdots+\left(5^{19}+5^{20}\right)\)
\(=5\left(1+5\right)+5^3\left(1+5\right)+\cdots+5^{19}\left(1+5\right)\)
\(=6\left(5+5^3+\cdots+5^{19}\right)\) ⋮6
c: \(C=5+5^2+5^3+\cdots+5^{20}\)
\(=\left(5+5^2+5^3+5^4\right)+\left(5^5+5^6+5^7+5^8\right)+\cdots+\left(5^{17}+5^{18}+5^{19}+5^{20}\right)\)
\(=5\left(1+5+5^2+5^3\right)+5^5\left(1+5+5^2+5^3\right)+\cdots+5^{17}\left(1+5+5^2+5^3\right)\)
\(=\left(1+5+5^2+5^3\right)\left(5+5^5+\cdots+5^{17}\right)=156\cdot\left(5+5^5+\cdots+5^{17}\right)\)
\(=13\cdot12\cdot\left(5+5^5+\cdots+5^{17}\right)\) ⋮13
Bài 2:
a: \(B=3+3^2+3^3+\cdots+3^{120}\)
\(=3\left(1+3+3^2+3^3+\cdots+3^{119}\right)\) ⋮3
b: \(B=3+3^2+3^3+\cdots+3^{120}\)
\(=\left(3+3^2\right)+\left(3^3+3^4\right)+\cdots+\left(3^{119}+3^{120}\right)\)
\(=3\left(1+3\right)+3^3\left(1+3\right)+\cdots+3^{119}\left(1+3\right)\)
\(=4\left(3+3^3+\cdots+3^{119}\right)\) ⋮4
c: \(B=3+3^2+3^3+\cdots+3^{120}\)
\(=\left(3+3^2+3^3\right)+\left(3^4+3^5+3^6\right)+\cdots+\left(3^{118}+3^{119}+3^{120}\right)\)
\(=3\left(1+3+3^2\right)+3^4\left(1+3+3^2\right)+\cdots+3^{118}\left(1+3+3^2\right)\)
\(=13\left(3+3^4+\cdots+3^{118}\right)\) ⋮13
Bài 1:
a: \(A=2+2^2+2^3+\ldots+2^{20}\)
\(=2\left(1+2+2^2+\cdots+2^{19}\right)\) ⋮2
b: \(A=2+2^2+2^3+\ldots+2^{20}\)
\(=\left(2+2^2\right)+\left(2^3+2^4\right)+\cdots+\left(2^{19}+2^{20}\right)\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+\cdots+2^{19}\left(1+2\right)\)
\(=3\left(2+2^3+\cdots+2^{19}\right)\) ⋮3
c: \(A=2+2^2+2^3+\ldots+2^{20}\)
\(=\left(2+2^2+2^3+2^4\right)+\left(2^5+2^6+2^7+2^8\right)+\cdots+\left(2^{17}+2^{18}+2^{19}+2^{20}\right)\)
\(=2\left(1+2+2^2+2^3\right)+2^5\left(1+2+2^2+2^3\right)+\cdots+2^{17}\left(1+2+2^2+2^3\right)\)
\(=15\left(2+2^5+\ldots+2^{17}\right)=5\cdot3\cdot\left(2+2^5+\cdots+2^{17}\right)\) ⋮5
Bài 1:
a; A = 2 + \(2^2\) + 2\(^3\) + ... + 2\(^{20}\)
A = 2 x (1+ 2+ 2\(^2\) + ... + 2\(^{19}\))
A ⋮ 2(đpcm)
b; A = 2 + \(2^2\) + 2\(^3\) + ... + 2\(^{20}\)
Xét dãy số: 1; 2;...; 20 đây là dãy số cách đều với khoảng cách là:
2 - 1 = 1
Số số hạng của dãy số trên là:
(20 - 1) : 1+ 1 = 20(số)
Vì 20 : 2 = 10
Vậy nhóm hai số hạng liên tiếp của A vào nhau khi đó ta có:
A = (2+ 2\(^2\)) + (2\(^3\) + 2\(^4\)) + ... + (2\(^{19}+\) 2\(^{20}\))
A = 2.(1 + 2) + 2\(^3\).(1+ 2) + ... + 2\(^{19}\) .(1 + 2)
A = 2.3 + 2\(^3\).3 + ... + 2\(^{19}\).3
A = 3.(2+ 2\(^3\) + ... + 2\(^{19}\))
A ⋮ 3 (đpcm)
c; A = 2 + \(2^2\) + 2\(^3\) + ... + 2\(^{20}\)
Xét dãy số: 1; 2; 3;...; 20
Dãy số trên có 20 số hạng:
Vì 20 : 4 = 5
Vậy nhóm 4 hạng tử của A thành một nhóm khi đó:
A = (2+ 2\(^2\) + 2\(^3\) + 2\(^4\)) + ... + (2\(^{17}+2^{18}+2^{19}+2^{20}\))
A = 2.(1 + 2 + 2\(^2\) + 2\(^3\)) + ... + 2\(^{17}\).(1 + 2 + 2\(^2\) + 2\(^3\))
A = (1+ 2 +2\(^2\) + 2\(^3\)).(2+ ...+ 2\(^{17}\))
A = (1 + 2 + 4 + 8).(2+ ...+ 2\(^{17}\))
A = (3+ 4 + 8).(2+ ...+ 2\(^{17}\))
A = (7 + 8)(2+ ...+ 2\(^{17}\))
A = 15.(2+ ...+ 2\(^{17}\))
A ⋮ 5(đpcm)

\(\dfrac{15}{34}+\dfrac{1}{3}+\dfrac{19}{34}-\dfrac{4}{3}+\dfrac{3}{7}=\left(\dfrac{15}{34}+\dfrac{19}{34}\right)+\left(\dfrac{1}{3}-\dfrac{4}{3}\right)+\dfrac{3}{7}=1-1+\dfrac{3}{7}=\dfrac{3}{7}\)

Ta có: \(10A=\frac{10^{21}-60}{10^{21}-6}=\frac{10^{21}-6-54}{10^{21}-6}=1-\frac{54}{10^{21}-6}\)
\(10B=\frac{10^{22}-60}{10^{22}-6}=\frac{10^{22}-6-54}{10^{22}-6}=1-\frac{54}{10^{22}-6}\)
Ta có: \(10^{21}-6<10^{22}-6\)
=>\(\frac{54}{10^{21}-6}>\frac{54}{10^{22}-6}\)
=>\(-\frac{54}{10^{21}-6}<-\frac{54}{10^{22}-6}\)
=>\(-\frac{54}{10^{21}-6}+1<-\frac{54}{10^{22}-6}+1\)
=>10A<10B
=>A<B

Bài 23:
a+4b⋮13
=>10(a+4b)⋮13
=>10a+40b⋮13
=>10a+b+39b⋮13
mà 39b⋮13
nên 10a+b⋮13
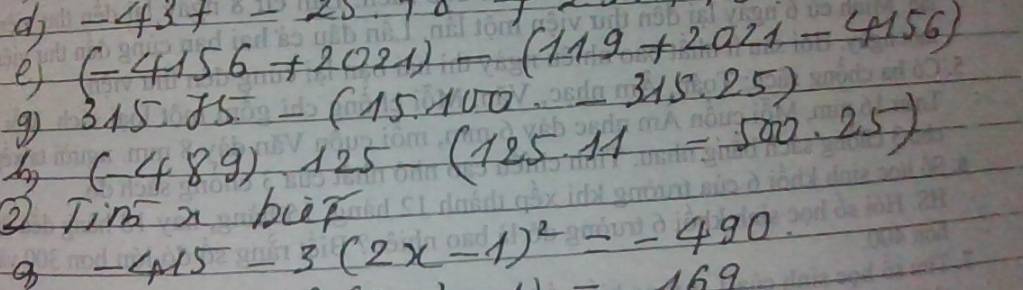
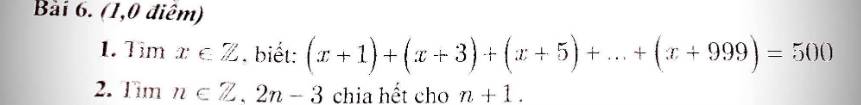
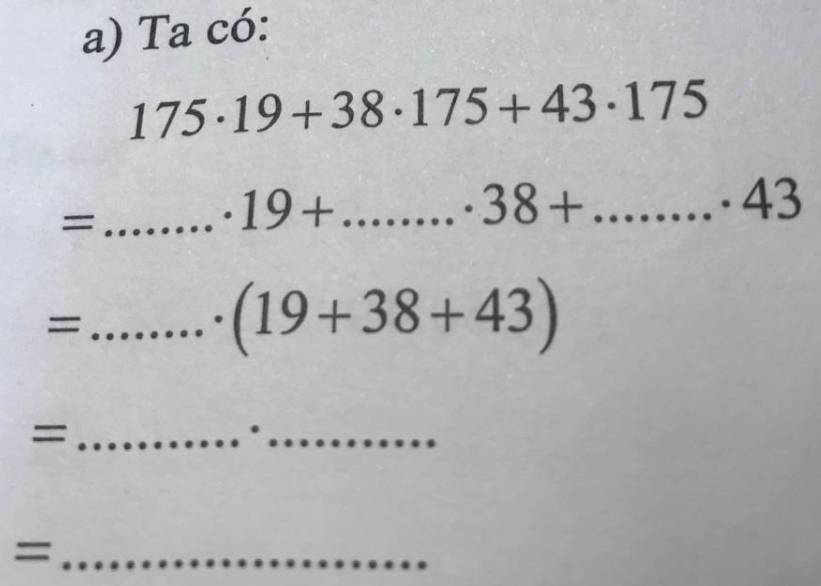
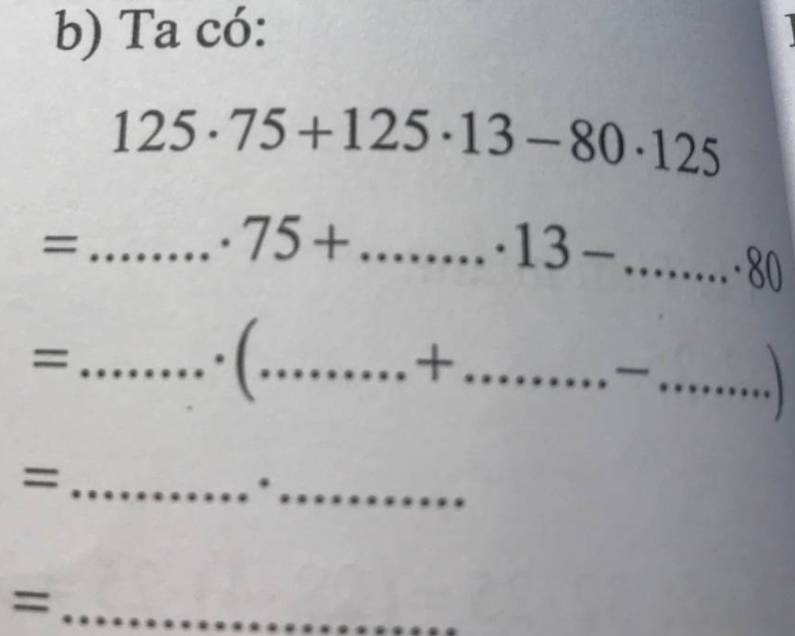
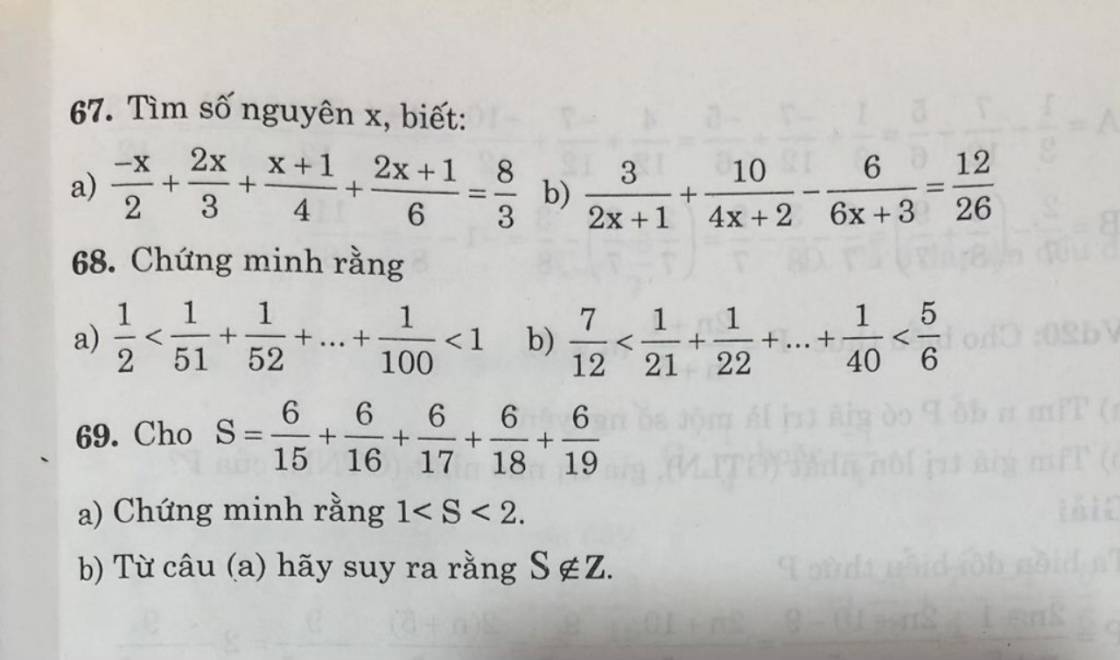





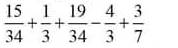


e: \(\left(-4156+2021\right)-\left(119+2021-4156\right)\)
\(=-4156+2021-119-2021+4156\)
\(=\left(-4156+4156\right)+\left(2021-2021\right)-119\)
=0+0-119
=-119
g: \(315\cdot75-\left(15\cdot100-315\cdot25\right)\)
\(=315\cdot75-15\cdot100+315\cdot25\)
\(=315\left(75+25\right)-15\cdot100\)
\(=315\cdot100-15\cdot100=300\cdot100=30000\)
h: \(\left(-489\right)\cdot125-\left(125\cdot11-500\cdot25\right)\)
\(=-489\cdot125-125\cdot11+500\cdot25\)
\(=125\left(-489-11\right)+500\cdot25\)
\(=125\cdot\left(-500\right)+500\cdot25\)
\(=500\left(-125+25\right)\)
\(=500\cdot\left(-100\right)=-50000\)
Bài 2:
a: \(-415-3\left(2x-1\right)^2=-490\)
=>\(3\left(2x-1\right)^2+415=490\)
=>\(3\left(2x-1\right)^2=75\)
=>\(\left(2x-1\right)^2=25\)
=>\(\left[{}\begin{matrix}2x-1=5\\2x-1=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=6\\2x=-4\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)