NT
21
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
30 tháng 5 2022
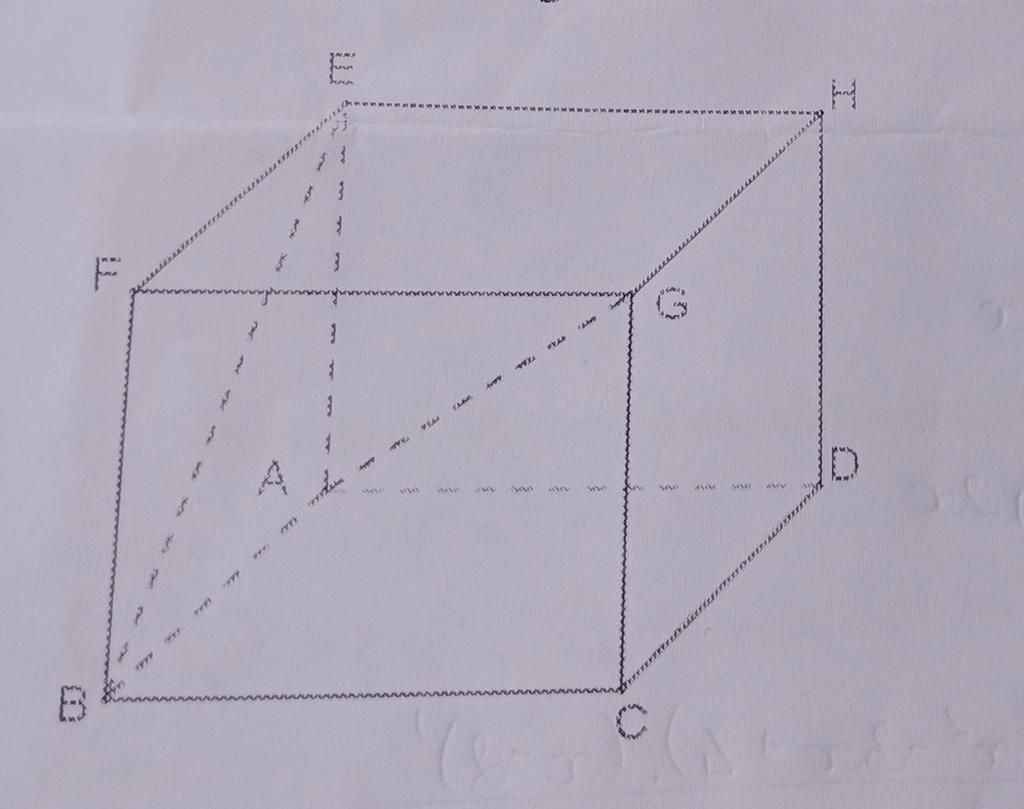
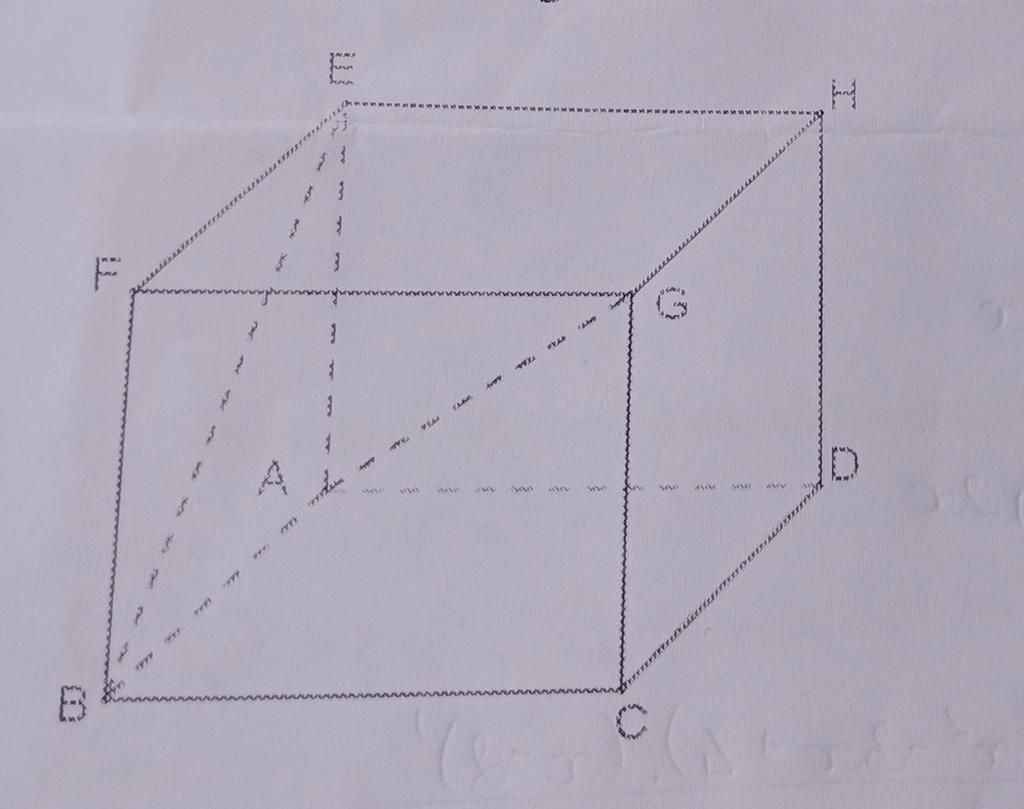
Đặt độ dài cạnh của hình lập phương là a
Ta có : \(\overrightarrow{AG}.\overrightarrow{BE}=\left(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AE}\right)\left(\overrightarrow{AE}-\overrightarrow{AB}\right)\)
⇒ \(\overrightarrow{AG}.\overrightarrow{BE}=\overrightarrow{AB}.\overrightarrow{AE}-AB^2+\overrightarrow{AD}.\overrightarrow{AE}-\overrightarrow{AD}.\overrightarrow{AB}+AE^2-\overrightarrow{AE}.\overrightarrow{AB}\)
Các tích vô hướng ở vế phải bằng 0 và AE = AB
⇒ \(\overrightarrow{AG}.\overrightarrow{BE}=0\) ⇒ AG ⊥ BE, tức góc giữa hai đường thẳng này bằng 900
18 tháng 2 2020
- Mỗi số tự nhiên cần lập là số tự nhiên có không quá 2 chữ số, được lập từ các chữ số 1, 2, 3, 4, 5, 6.
- Để lập được số tự nhiên như vậy, phải thực hiện một hành động trong hai hành động loại trừ nhau sau đây:
- Hành động 1: Từ các chữ số 1, 2, 3, 4, 5, 6, lập số tự nhiên có một chữ số. Có 6 cách để thực hiện hành động này.
- Hành động 2: Từ các chữ số 1, 2, 3, 4, 5, 6, lập số tự nhiên có hai chữ số.
- Vận dụng quy tắc nhân, ta tìm được: Có 62 = 36 cách để thực hiện hành động này.
- Theo quy tắc cộng suy ra số các cách để lập được các số tự nhiên kể trên là
6 + 36 = 42 (cách)
- => Qua trên suy ra từ các chữ số đã cho có thể lập được 42 số tự nhiên bé hơn 100.
16 tháng 8
Chọn mp(SBD) có chứa SD
B∈(SBD)
B∈(MBC)
Do đó: B∈(SBD) giao (MBC)(1)
M∈SO⊂(SBD)
M∈(MBC)
Do đó: M∈(SBD) giao (MBC)(2)
Tư (1),(2) suy ra (SBD) giao (MBC)=BM
Gọi E là giao điểm của BM va SD
=>E là giao điểm của SD và mp(MBC)
Chọn mp(SAD) có chứa SA
E∈MB⊂(MBC)
E∈ SD⊂(SAD)
Do đó: E∈(MBC) giao (SAD)
Xét (MBC) và (SAD) có
E∈(MBC) giao (SAD)
BC//AD
Do đó: (MBC) giao (SAD)=xy, xy đi qua E và xy//BC//AD
Gọi F là giao điểm của SA va xy
=>F là giao điểm của SA và mp(MBC)
Vì xy//AD
nên EF//AD
24 tháng 10 2016
Nếu mà không quá 1 em nữ => Không có em nữ nào tham gia.
=> 5 em trên là 5 em nam và chỉ có 1 cách chọn.
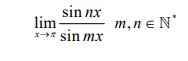
Cô hoài giả mạo !!!
Cô hoài giả mạo