Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xài bđt phụ mới cần phải chứng minh nhé
mà tau nhớ làm gì có Cô si dạng Engel ??? ._.

Trên đây nó ko cho đăng ảnh,mn chịu khó nhập link này vào nha:https://i.imgur.com/xQNntGH.png

K D H A B C
a) Xét tam giác ADC và tam giác BKC có:
\(\hept{\begin{cases}\widehat{C}\text{ chung}\\\widehat{BKC}=\widehat{ADC}\left(=90^{\text{o}}\right)\end{cases}}\Rightarrow\Delta ADC\approx\Delta BKC\)(g-g)
b) Xét tam giác BDM và tam giác BDH có :
\(\hept{\begin{cases}BD\text{ chung}\\\widehat{BDM}=\widehat{BDH}\left(=90^{\text{o}}\right)\\MD=DH\end{cases}}\Rightarrow\Delta BDM=\Delta BDH\left(c.g.c\right)\)
=> \(\widehat{BMD}=\widehat{BHD}\left(\text{góc tương ứng}\right)\)
=> \(\Delta MBH\text{ cân tại B}\)
c) Xét tam giác AHK và tam giác BMD có :
\(\hept{\begin{cases}\widehat{BMD}=\widehat{AHK}\left(=\widehat{BHD}\right)\\\widehat{BDM}=\widehat{HKA}\left(=90^{\text{o}}\right)\end{cases}\Rightarrow\Delta AKH\approx\Delta BMD\left(g-g\right)}\)
=> \(\Rightarrow\widehat{DBM}=\widehat{KAH}\text{ hay }\widehat{CBM}=\widehat{CAM}\)

a: Xet ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạngvới ΔAEC
b: Xet ΔIEB vuông tại E và ΔIDC vuông tại D có
góc EIB=góc DIC
=>ΔIEB đồng dạng với ΔIDC

a.
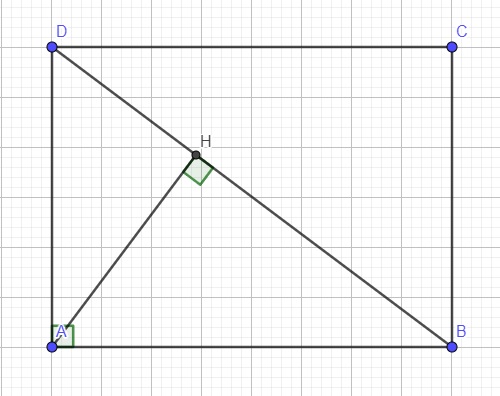
Do ABCD là hình chữ nhật \(\Rightarrow\widehat{HBA}=\widehat{CDB}\) (so le trong)
Xét hai tam giác HBA và CDB có:
\(\left\{{}\begin{matrix}\widehat{HBA}=\widehat{CDB}\left(cmt\right)\\\widehat{AHB}=\widehat{BCD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta HBA\sim\Delta CDB\left(g.g\right)\)
b.
Xét hai tam giác AHD và BAD có:
\(\left\{{}\begin{matrix}\widehat{ADB}\text{ chung}\\\widehat{AHD}=\widehat{BAD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta AHD\sim\Delta BAD\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{DB}=\dfrac{DH}{AD}\Rightarrow AD^2=DH.DB\)
c.
Áp dụng định lý Pitago cho tam giác vuông BAD:
\(DB=\sqrt{AD^2+AB^2}=\sqrt{BC^2+AB^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Theo chứng minh câu b:
\(AD^2=DH.DB\Rightarrow DH=\dfrac{AD^2}{DB}=\dfrac{BC^2}{DB}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
Áp dụng Pitago cho tam giác vuông AHD:
\(AH=\sqrt{AD^2-HD^2}=\sqrt{6^2-3,6^2}=4,8\left(cm\right)\)

Phổ thông?Có phải dạng này không nhỉ?
`(ax+by)^2<=(a^2+b^2)(x^2+y^2)`
`<=>a^2x^2+b^2y^2+2axby<=a^2x^2+a^2y^2+b^2x^2+b^2y^2`
`<=>a^2y^2-2axby+b^2x^2>=0`
`<=>(ay-bx)^2>=0` luôn đúng
Dấu "=" `<=>ay=bx<=>a/x=b/y`
vg ạ e cảm ơn