Q
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 4 2016
Số trang sách ngày thứ nhất Kiên đọc được là:
60 . \(\frac{1}{3}\)= 20 (trang)
Số trang sách còn lại sau ngày thứ nhất đọc là:
60 - 20 =40 (trang)
Số trang sách ngày thứ hai Kiên đọc được là:
40 . \(\frac{3}{5}\) =24 (trang)
Số trang sách ngày thứ ba Kiên đọc được là:
40 - 24=16 (trang)
Đáp số: 16 trang.
22 tháng 4 2016
Số trang ngày thứ nhất Kiên đọc là:
1 phần 3 nhân 60=20(trang)
Số trang còn lại là:
60-20=40(trang)
Số trang ngày thứ 2 đọc là:
3 phần 5 nhân 40=24(trang)
Số trang ngày thứ ba Kiên đọc là :
60-20-24=16 (trang)
đáp số :16 trang
CM
20 tháng 7 2019
Chọn đáp án D
Phương pháp
Đồ thị hàm số y=f(x) và đường thẳng y=g(x) có duy nhất 1 điểm chung ⇒ phương trình hoành độ giao điểm f(x)=g(x) có nghiệm duy nhất.
Cách giải
Phương trình hoành độ giao điểm của đồ thị hai đồ thị hàm số là
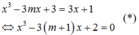
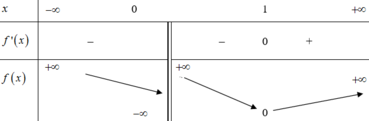
Hai đồ thị hàm số có duy nhất 1 điểm chung khi và chỉ khi phương trình (*) có nghiệm duy nhất
27 tháng 4 2016
Gọi x là số trang của quyển sách
Số trang sách ngày thứ nhất đọc là \(\frac{1}{3}x\)
Số trang sách ngày thứ hai đọc là \(\frac{5}{8}\left(x-\frac{x}{3}\right)=\frac{5x}{12}\)
Theo đề bài ta có phương trình:
\(x-\frac{x}{3}-\frac{5x}{12}=90\)
<=> 12x-4x-5x=1080
<=> 3x=1080
<=> x=360(trang)
Vậy quyển sách có 360 trang
14 tháng 6 2019
7/ Em sửa lại đề ạ
Cho hai số thực dương a, b thỏa mãn a+b=4ab
Chứng minh rằng \(\frac{a}{4b^2+1}+\frac{b}{4a^2+1}\ge\frac{1}{2}\)
Đổi biến \(\left(a,b\right)\rightarrow\left(\frac{1}{x},\frac{1}{y}\right)\)
Từ giả thiết => x+y=4
Ta có: BĐT cần CM tương đương với:
\(\frac{\frac{1}{x}}{\frac{4}{y^2}+1}+\frac{\frac{1}{y}}{\frac{4}{x^2}+1}\ge\frac{1}{2}\)\(\Leftrightarrow\frac{y^2}{x\left(4+y^2\right)}+\frac{x^2}{y\left(4+x^2\right)}\ge\frac{1}{2}\left(1\right)\)
Áp dụng BĐT Schwarz, ta có:
∑\(\frac{x^2}{y\left(4+x^2\right)}\ge\frac{\left(x+y\right)^2}{4\left(x+y\right)+xy^2+x^2y}=\frac{16}{16+xy^2+x^2y}\)
Ta chỉ cần chứng minh:
\(xy^2+x^2y\le16\Leftrightarrow xy^2+x^2y\le\frac{1}{4}\left(x+y\right)^3\)
\(\Leftrightarrow xy^2+x^2y\le x^3+y^3\)(luôn đúng)
Do đó (1) đúng. BĐT được chứng minh. Dấu "=" xảy ra khi x=y=2⇔a=b=\(\frac{1}{2}\)
14 tháng 6 2019
6. (chuyên Hòa Bình)
Cho các số dương x, y, z thỏa mãn: xy+zx+4yz=32
Tìm giá trị nhỏ nhất của\(P=x^2+16y^2+16z^2\)
Áp dụng bất đẳng thức Cauchy cho ba số dương x,y,z ta có
\(\hept{\begin{cases}8y^2+\frac{1}{2}x^2\ge2\sqrt{8y^2.\frac{1}{2}x^2}=4xy\\8z^2+\frac{1}{2}x^2\ge2\sqrt{8z^2.\frac{1}{2}x^2}=4xz\\8y^2+8z^2\ge2\sqrt{8y^2.8z^2}=16yz\end{cases}}\)
Cộng từng vế của ba bđt trên ta có
\(P\ge4\left(xy+xz+4yz\right)=4.32=128\)
BH
2
27 tháng 1 2022
\(\Leftrightarrow-5x-1-\dfrac{1}{2}x+\dfrac{1}{3}-\dfrac{3}{2}x+\dfrac{5}{6}=0\)
\(\Leftrightarrow-7x+\dfrac{1}{6}=0\)
=>7x=1/6
hay x=1/42
Là sao, giải thích đề bài đi chớ.
đề bài là sao đây