Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đa thức biểu thị diện tích phần tăng thêm của miếng bìa là:
\(\dfrac{1}{2}\cdot\left(6+x\right)\cdot\left(8+y\right)-\dfrac{1}{2}\cdot6\cdot8\)
\(=\dfrac{1}{2}\cdot\left(48+6y+8x+xy\right)-3\cdot8\)
\(=24+3y+4x+\dfrac{xy}{2}-24\)
\(=3y+4x+\dfrac{xy}{2}\)
b) Phần diện tích tăng thêm là:
\(3\cdot4+4\cdot2+\dfrac{2\cdot4}{2}=24\left(cm^2\right)\)
a) Diện tích tam giác sau khi tăng thêm:
(6 + x).(8 + y) : 2
= (48 + 6y + 8x + xy) : 2
= 24 + 3y + 4x + xy/2
Diện tích phần tăng thêm:
24 + 3y + 4x + xy/2 - 6.8:2
= 4x + 3y + xy/2 (cm)²
b) Khi x = 2 và y = 4 thì diện tích phần tăng thêm là:
4.2 + 3.4 + 2.4/2
= 8 + 12 + 4
= 24 (cm²)

Diện tích hình tam giác vuông ban đầu là: \(\dfrac{1}{2}.6.8 = 24\left( {c{m^2}} \right)\)
Độ dài các cạnh của hình vuông sau khi tăng độ dài là: x + 6 (cm); y + 8 (cm)
Diện tích tam giác vuông sau khi tăng độ dài là: \(\dfrac{1}{2}\left( {x + 6} \right).\left( {y + 8} \right) = \dfrac{{{xy}}}{2} + 4x + 3y + 24\left( {c{m^2}} \right)\)
Đa thức biểu thị phần diện tích tăng thêm của miếng bìa là: \(\dfrac{{{xy}}}{2} + 4x + 3y + 24 - 24 = \dfrac{{{xy}}}{2} + 4x + 3y\left( {c{m^2}} \right)\)
Vậy đa thức biểu thị phần diện tích tăng thêm của miếng bìa là: \(\dfrac{{{xy}}}{2} + 4x + 3y\left( {c{m^2}} \right)\)

Bài 4:
1)
a) Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔHBA\(\sim\)ΔABC(g-g)
b) Xét ΔABC có AH là đường cao ứng với cạnh huyền BC, ta có:
\(S_{ABC}=\dfrac{AH\cdot BC}{2}\)(1)
Ta có: ΔABC vuông tại A(gt)
nên \(S_{ABC}=\dfrac{AB\cdot AC}{2}\)(2)
Từ (1) và (2) suy ra \(AH\cdot BC=AB\cdot AC\)
c) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=12^2+16^2=400\)
hay BC=20(cm)
Ta có: \(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot20=12\cdot16=192\)
hay AH=9,6(cm)
Bài 3:
Gọi x(cm) là độ dài cạnh góc vuông nhỏ(Điều kiện: x>0)
Độ dài cạnh góc vuông lớn là: x+2(cm)
Theo đề, ta có phương trình:
\(\dfrac{\left(x-3\right)\left(x+2+4\right)}{2}=\dfrac{x\left(x+2\right)}{2}+30\)
\(\Leftrightarrow\left(x-3\right)\left(x+6\right)=x\left(x+2\right)+30\)
\(\Leftrightarrow x^2+3x-18-x^2-2x=30\)
\(\Leftrightarrow x-18=30\)
hay x=48(thỏa ĐK)
Vậy: Chu vi của tam giác vuông đó là:\(98+2\sqrt{1201}\left(cm\right)\)

3\(a^2\)+4a+1=3\(a^2\)+3a+a+1
=(3\(a^2\)+3a)+(a+1)
=3a(a+1)+(a+1)
=(a+1)(3a+1)

Áp dụng Pytago: \(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
Vì AM là tt ứng cạnh huyền BC nên \(AM=\dfrac{1}{2}BC=5\left(cm\right)\)
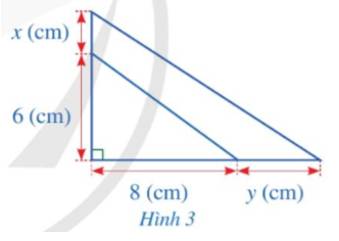
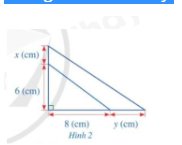
Diện tích tam giác vuông miếng bìa cứng sau khi tăng là :
\(\left(x+6\right)\left(8+y\right)\left(cm^2\right)\)
Đa thức biểu thị diện tích phần tăng thêm của miếng bìa :
\(\left(x+6\right)\left(8+y\right)-6.8\)
\(=8x+xy+48+6y-48\)
\(=8x+6y+xy\left(cm^2\right)\)