Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
Gọi (Q) là mặt phẳng đi qua M (2;2; -3) và song song với mặt phẳng (P).
Suy ra (Q):2x+y+z-3=0.
Do Δ // (P) nên Δ ⊂ (Q)).
D (N, Δ) đạt giá trị nhỏ nhất ó Δ đi qua N', với N' là hình chiếu của N lên (Q).
Gọi d là đường thẳng đi qua N và vuông góc (P),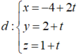 
Ta có N’ ∈ d => N' (-4+2t;2+t;1+t); N’ ∈ (Q) => t = 4/3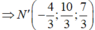 
cùng phương 
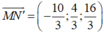
Do |a|, |b| nguyên tố cùng nhau nên chọn 
Vậy |a| + |b| + |c| = 15.
Chọn D.
Phương trình đường thẳng d có hệ số góc k và đi qua I(1; 2) là d: y = k(x - 1) + 2.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d:
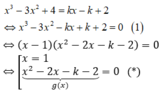
Để d cắt (C) tại ba điểm phân biệt ⇔ Phương trình (*) có hai nghiệm phân biệt x1; x2 khác 1.
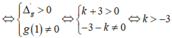
Hơn nữa theo Viet ta có
nên I là trung điểm AB.
Vậy chọn k > -3, hay k ∈ (-3;+∞).
Chọn D
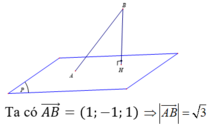
Gọi H là hình chiếu của B trên mặt phẳng (P) khi đó ta có BH là khoảng cách từ điểm B đến mặt phẳng (P). Ta luôn có BH ≤ AB do đó khoảng cách từ B đến mặt phẳng (P) lớn nhất khi H ≡ A, khi đó 
là véc tơ pháp tuyến của mặt phẳng (P)
Vậy phương trình mặt phẳng (P) đi qua A (-1; 2; 4) và có véc tơ pháp tuyến 
là x - y + z - 1 = 0
Vậy khoảng cách từ điểm O đến mặt phẳng (P) là:
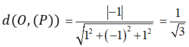
Phương trình đường thẳng d; y=k(x-1)+2.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d:
x3-3x2+4= k(x-1)+2. Hay x3-3x2-kx+k+2= 0 (1)
⇔
(
x
-
1
)
(
x
2
-
2
x
-
k
-
2
)
=
0
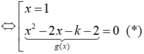
( C) cắt d tại ba điểm phân biệt khi và chỉ khi phương trình có hai nghiệm phân biệt x1; x2 khác 1
⇔ ∆ ' g > 0 g ( 1 ) ≠ 0 ⇔ k + 3 > 0 - 3 - k ≠ 0 ⇔ k > - 3
Hơn nữa theo Viet ta có
x 1 + x 2 = 2 = 2 x I y 1 + y 2 = k ( x 1 + x 2 ) - 2 k + 4 = 4 = 2 y I
nên I là trung điểm AB.
Vậy chọn k> -3, hay k ∈ (-3; +∞). Do đó có vô số giá trị k nguyên thỏa mãn yêu cầu bài toán.
Chọn D.
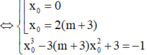
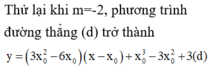
khó quá
Khó thì để cho người khác còn làm !