Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi M', d' và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua O.
Dùng biểu thức tọa độ của phép đối xứng qua gốc tọa độ ta có :
M′ = (2; −3), phương trình của d′: 3x – y – 9 = 0, phương trình của đường tròn (C′): x 2 + y 2 − 2 x + 6 y + 6 = 0 .
b) Gọi M', d' và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua I .
Vì I là trung điểm của MM' nên M′ = (4;1)
Vì d' song song với d nên d' có phương trình 3x – y + C = 0.
Lấy một điểm trên d, chẳng hạn N(0; 9).
Khi đó ảnh của N qua phép đối xứng qua tâm I là N′(2; −5).
Vì N' thuộc d nên ta có 3.2 − (−5) + C = 0. Từ đó suy ra C = -11.
Vậy phương trình của d' là 3x – y – 11 = 0.
Để tìm (C'), trước hết ta để ý rằng (C) là đường tròn tâm J(−1; 3),
bán kính bằng 2. Ảnh của J qua phép đối xứng qua tâm I là J′(3; 1).
Do đó (C') là đường tròn tâm J' bán kính bằng 2. Phương trình của (C') là x − 3 2 + y − 1 2 = 4 .

Giao của d với trục \(Ox\) là điểm \(A\left(3;0\right)\). Phép tịnh tiến phải tìm có vectơ tịnh tiến \(\overrightarrow{v}=\overrightarrow{AO}=\left(-3;0\right)\). Đường thẳng d' song song với d đi qua gốc tọa độ nên nó có phương trình \(3x-y=0\)

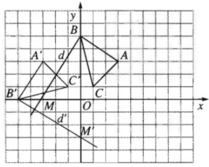
a) Lấy hai điểm A(0;4) và B(2;0) thuộc d. Gọi A′, B′ theo thứ tự là ảnh của A và B qua phép vị tự tâm O tỉ số k = 3. Khi đó ta có
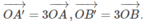
Vì O A → = ( 0 ; 4 ) nên O A ' → = ( 0 ; 12 ) . Do đó A′ = (0;12).
Tương tự B′ = (6;0); d1 chính là đường thẳng A'B' nên nó có phương trình:
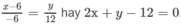
b) Có thể giải tương tự như câu a) .
Sau đây ta sẽ giải bằng cách khác.
Vì d 2 / / d nên phương trình của d 2 có dạng 2x + y + C = 0.
Gọi A′ = (x′;y′) là ảnh của A qua phép vị tự đó thì ta có:
I A ' → = − 2 I A → hay x′ + 1 = −2, y′ − 2 = −4
Suy ra x′ = −3, y′ = −2
Do A' thuộc d 2 nên 2.(−3) – 2 + C = 0.
Từ đó suy ra C = 8
Phương trình của d 2 là 2x + y + 8 = 0

Giao của d với trục Ox là điểm A(3;0). Phép tịnh tiến phải tìm có vectơ tịnh tiến v → = O A → = ( − 3 ; 0 ) . Đường thẳng d' song song với d và đi qua gốc tọa độ nên nó có phương trình 3x – y = 0.

Gọi M′, d′ và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua trục Ox .
Khi đó M′ = (3;5) . Để tìm ta viết biểu thức tọa độ của phép đối xứng qua trục:
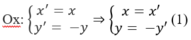
Thay (1) vào phương trình của đường thẳng d ta được 3x′ − 2y′ − 6 = 0.
Từ đó suy ra phương trình của d' là 3x − 2y – 6 = 0
Thay (1) vào phương trình của (C) ta được x ' 2 + y ' 2 − 2 x ′ + 4 y ′ − 4 = 0 .
Từ đó suy ra phương trình của (C') là x − 1 2 + y − 2 2 = 9 .
Cũng có thể nhận xét (C) có tâm là I(1; −2), bán kính bằng 3,
từ đó suy ra tâm I' của (C') có tọa độ (1;2) và phương trình của (C') là x − 1 2 + y − 2 2 = 9